Reference no: EM132360187

Advanced Mathematics Questions -

Question 1 -

The figure shows a cross-section of a copper alloy material embedded in a perfectly insulating material. Two sides are open and subjected to imposed temperatures. On the left side the temperature is measured at the points given in the table above. Unfortunately one of the temperature sensors was corrupt and did not give a reliable measure (blank). Also on the bottom side, the temperature was measured, but the measurements indicated a nearly constant value of 10^oC. You can assume that the above 2D-figure is representative for the situation.

Questions:

1. You know that the Laplace equation can be used to calculate the temperature in the copper alloy body and that the above problem is a boundary value problem. Explain what this means and demonstrate this by identifying the different types of boundaries for the example above and the boundary values you will impose when you solve the Laplace equation for the equipotential (temperature) and for stream function.

2. Assume that Δz = Δy. Assume that you discretize the domain using 1Δy as standard unit in the y-direction and 1Δz as standard unit in the z-direction. Set-up the matrix system to solve the Laplace equation for the stream function. You do not need to write down all coefficients of the matrix, but make sure that you show one point for each of the different numerical stencils that you will need to use. Make sure that you include the point at z = 3m on the left boundary. Also make sure that you give the correct dimension of the matrix.

3. Without doing any calculations, make a sketch of what you expect the solution will look like.

Question 2 -

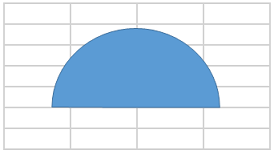
The cross-section of containers has the shape of a semi-circle with radius R (e.g. R = 0.5m). You can consider that the height of the half cylinder is H (e.g. H=0.8 m).

Questions:

1. Draw unit vectors normal to the outer contour of the cross section (perpendicular to the height, see figure).

2. Give the unit normal vectors to the different surfaces of this body in cylindrical coordinates.

3. Give the unit normal vectors to the different surfaces of this body in cartesian coordinates.

Question 3 -

Using the forward in time central in space (FTCS) finite difference approximation for the advection part in the advection-diffusion, is not always a good idea. The equation is unconditionally unstable far advection only. The Lax and modified Lax scheme were developed and tackled the problem by basically introducing numerical diffusion in the finite difference approximation, resulting in the following formula:

C_n,m+1 = α/2(C_n+1,m + C_n-1,m) + (1 - α)C_n,m - uΔt/2Δx (C_n+1,m - C_n-1,m)

Numerical stability analysis showed that the numerical scheme for advection is stable under the following conditions:

σ² ≤ α where 0 ≤ α ≤ 1 and σ = uΔt/Δx

For the current application α is set to 0.5.

Questions:

1. Choose a value of σ. Take a value as large as possible while still obeying the stability criteria.

2. Apply your scheme to a simple example in which the advection velocity is set to 1m/s and in which the initial condition is given by a constant concentration of 5mg/l. The problem at hand can be represented by a problem in the x-direction only. The domain of interest is 500m long and the space step Δx is set to 50m. Measurements at the upstream end are made every minute. Until time T=T₀, the concentration at the upstream end does not differ much from the background concentration (difference less than 1mg/l). However some changes in the upstream concentration were measured 10 minutes later (thus from t = T₀ onwards). The concentration almost linearly increased from 5mg/l to 55mg/l over the next 10 minutes, and then gradually (assume linearly) decreased again to 5mg/l over the next 20 minutes.

3. Do the calculation by hand for the first two time-steps after the concentration started changing. Discuss clearly the assumption you make. (To limit the calculation time needed, calculate the first three or 4 points in space starting at the upstream end).

4. Since it is a pure advection problem, it is relatively easy to draw an 'exact' solution for any time t. Do this for t = T₀ + 25'. Draw this exact solution.

5. What would change if diffusion would play a role? Draw a sketch of the solution you obtained in question 4 (qualitatively) if diffusion would be added.