Reference no: EM131282581

You must observe the following requirements (for all homework submitted in this course):

All programs should be literate, i.e., easily understandable by a human (say, your grader) and follow the Java Style Guidelines for CS112 posted on the class web site;

All files for this homework should be submitted using WebSubmit, following the instructions on the class web site;

You may not use data structure libraries such as ArrayList, since we are learning to write Java from the ground up and you must learn how these libraries are built; however, you are free to use (unless specifically directed otherwise) the basic libraries String, Character, Scanner, and Math; for this assignment, you may also use Double.parseDouble(....);

You may freely use code from the class web site, the textbook, or lecture (unless specifically directed otherwise) as long as you cite the source in your comments; but you may NEVER use code from the web or other students' programs.

Part A: Analytical Problems

Before getting started on the remaining problems, review the lecture and textbook materials on binary search trees and recursion. The following problems have to do with the BST in this diagram:

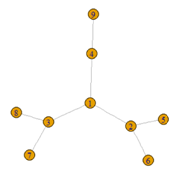
In these problems, draw your solution trees in "ASCI art" sideways, so the tree above would be rendered as:

            46
        43
            31
    19
        17
11
            10
        8
    6
 
            5
        4

1. : For this tree, give the (a) size, (b) depth of the node 31, (c) height, (d) length of the path from 11 to 49, and (e) list of all leaf nodes.

2. (a) Draw the result of inserting the keys 15, 7, 16, 12, & 13 into this tree; (b) assuming we can only insert integers, and no duplicates, into the original tree, what keys could possibly be inserted to the left of 31?

3. (a) Draw the result of taking the tree in the diagram and deleting the root three times using the deletion algorithm from lecture and the web (i.e., when deleting a node with two children, move up the least element from the right subtree); (b) suppose we do not wish to unbalance the tree by deleting from the same side each time, and we decide that we will alternately delete from the right, left, right, left, etc. (starting with the right); delete the root of the tree in the diagram 4 times using this new strategy and show the resulting tree.

4. Let us call a tree "perfect" if it is a perfect triangle, i.e.,

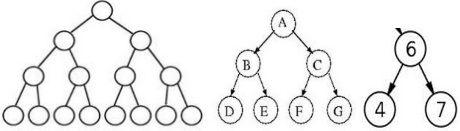
Suppose H is the height of a perfect binary tree, and N the number of nodes; (a) express H as a function of N, and (b) N as a function of H.

5.: Suppose we are going to insert the letters A, B, C, and D, into an initially empty BST. If we insert them in order, we get a pathological tree which is really just a linked list (and whose worst case time to find a node is linear, i.e., Theta(N)). But there are many different worst cases! (a) List 5 more of the the possible worst cases (hint: there are 8 in all!). Now suppose we have the letters A, B, C, D, E, F, and G. We would like to have a perfect tree which has the shape of a perfect triangle: for example, we could insert in the order D, B, F, A, C, E, G. (b) List 5 more of the possible insertion orders that would give you a complete binary search tree.