Draw Nyquist diagram of the closed loop system

Reference no: EM132358839

Question 1 - A digital filter is defined by the difference equation;

y(k) - 1.6065y(k - 1) + 0.6065y(k - 2) = u(k - 1) + u(k - 2)

a. Obtain the discrete time transfer function for the digital filter G(z).

b. Study how the filter G(z) handles the input signal u(n) = (-1)ⁿ1(n).

c. Plot the Bode diagram of G(z) using Matlab include the code in your answer. Validate the result from part a.

d. If G(z) is included in a closed loop system shown in Figure Q1, plot the Bode diagram for the closed loop system using Matlab and find phase margin and gain margin of the closed loop system. Assume K=1 and include the code in your answer.

e. Plot step response of the closed loop system and specify the overshoot, risetime, settling time and steady-state of the response.

Question 2 - a. Draw root locus diagram of the closed loop system shown in Figure Q1 and find the values of 0 < K < ∞ the system is stable.

b. Draw Nyquist diagram of the closed loop system shown in Figure Q1 and find the values of 0 < K < ∞ where the system is stable.

c. Draw the Bode diagram of the closed loop system shown in Figure Q1 and find the values of 0 < K < ∞ where the system is stable.

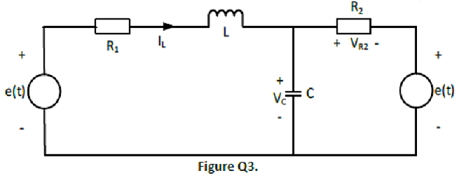
Question 3 - Find the following for the circuit shown in Figure Q3.

a. Write the continuous time state equations of the circuit.

b. Find transfer function G(s) = V_{R_2}(s)/E(s) where E(s) = L{e(t)}.

c. Assume C = 0.2 F, L = 2 H, R₁ = 100 Ω, R₂ = 50 Ω. Find the ZOH equivalent discrete system in part a if sampling time is 1 s.

d. Find the transfer function G(z) in part b.

e. Find the zero-state step response (steady state) of the circuit to the input {e(n)}.

f. Find the zero input or transient response of the circuit when initial condition of the circuit is: V_c(0) = 4 V, I_L(0) = 0.25 A.

Question 4 - a. Using pole-zero placement, design a filter G(z) that filters out the frequency ω₀ = 2π/3 and at frequency ω = 0, G(1) = 1.5.

b. Show that if u(n) is the input and y(n) is the output of the filter G(z) in part a, y(n) can be written as, y(n) = b₀u(n) - b₁u(n - 1) - b₂u(n - 2) and find the coefficient b₀, b₁ and b₂.

c. Show that if u(n) = cosω₀n (ω₀ = 2π/3) is the input to G(z) then the output y(n) = 0. (Hint: use the equation cos A + cos B = 2 cos (A+B)/2 cos (A-B)/2).

d. Find the relationship between the phase angle of the filter and the frequency ω.

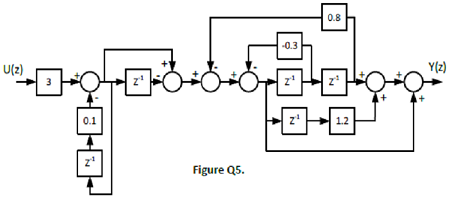
Question 5 - Answer the following questions about the diagram of a digital filter shown in Figure Q5.

a. Find the discrete time state equation of the diagram.

b. Find the transfer function of the diagram.

c. Find the inverse z-transform of the transfer function you found in part b.

Reference no: EM132358839

Questions Cloud

What were some of the pros and cons mentioned : What was the most surprising thing you learned from the movie? What were some of the pros and cons mentioned?

Which emphasizes happiness and flourishing : In this module's learning, you were introduced to Aristotle's idea of eudaimonia, which emphasizes happiness and flourishing.

Provide an audit of personal skills : Provide an audit of personal skills, discipline knowledge and experience (a brief write-up of your expertise etc.) that you bring to the consulting team

Stand out in terms of leadership and empowerment : Share an example of a leader you feel empowers others. What are some traits that stand out in terms of leadership and empowerment?

Draw Nyquist diagram of the closed loop system : Draw Nyquist diagram of the closed loop system shown in Figure Q1 and find the values where the system is stable

Writing persuasive essay-does title capture central focus : Persuasive Essay- Does the writing meet the assignment requirements and engage the audience? Does the title capture the central focus?

Observe how people use the space : Observe how people use the space. Sketch where people stand, sit, or congregate-and use arrows to indicate people's changing positions and paths.

Discuss the major categories of reimbursements : Outline and discuss the major categories of reimbursements and costs in a health care organization. How do they influence each other?

Mitigate effects of financial impact to your organization : Your community has experienced unemployment rates of approximately 9%. What can be done to mitigate the effects of the financial impact to your organization?

User Account

All Pages