Draw a sketch to represent the stress distribution

Assignment Help Mechanical Engineering

Reference no: EM13161334

Question 1: Bending about two axes

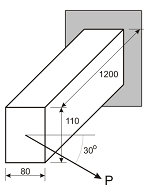
The load P = 2 kN is applied to the end of rectangular section cantilever beam shown at the right. The load acts within the plane of the end face and at an angle of 30° as illustrated. (a) Calculate the magnitude of the moment acting at the build-in (fixed) end and specify the orientation of the moment vector relative to the principal centroidal axes of the section with the aid of a sketch. (b) Determine the stresses at each corner of the built-in (fixed) end of the beam. (c) Specify the orientation of the neutral axis relative to the principal centroidal axes of the section using a sketch. (d) Draw a sketch to represent the stress distribution on the section.

943_Draw a sketch to represent the stress distribution.png

Question 2: Principal centroidal axes

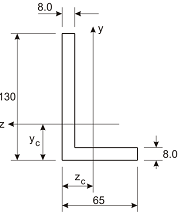
Consider the unequal angle section illustrated in the figure to the right. (a) Calculate the location of the centroid as defined byzc and yc; (b) Determine the values of Iz, Iy, and Izy for the axes illustrated; (c) Calculate the values of Imax and Imin; (d) Show your calculated orientation of the principal centroidal axes (PCAs) on a sketch of the section, noting the axes associated with Imax and Imin values; and (e) Compare your calculated values for Iz, Iy, and the orientation of the PCAs with available data for the section L 130 x 65 x 8 listed in the tables: European unequal angles.jpg, and discuss the differences.

1309_Draw a sketch to represent the stress distribution1.png

Question 3: Asymmetric bending analysis

This question requires the analysis of data presented on the Study Desk under the heading, Assignment 3 Demonstration. For this demonstration, an unequal angle is clamped at one end and is subjected to a state of bending. Data on the section properties is provided on the Study Desk.

Analysis of the images of the end of the beam is to be performed for comparison with the theoretical results.

In beam bending, the neutral axis defines the orientation of the plane along which direct (normal) strains (and hence, stresses) are zero. The magnitude of the direct strain increases in direct proportion to the distance from the neutral axis and hence the beam deflects in a direction perpendicular to the orientation of the neutral axis.

Required analysis tasks:

(a) Produce a sketch specifying the magnitude and angle of the moment vector relative to the PCAs for the given orientation of the section and the loading.

(b) Using the specified second moments of area and the PCA orientations, determine the expected angle of the neutral axis relative to the horizontal plane and show the neutral axis on a correctly oriented sketch of the section.

(c) Determine the magnitude and location of the expected maximum compressive and tensile stresses within the section when the load is applied.

(d) Analyse the two photographs and account for the measured support rotation effect to specify the horizontal and vertical deflection of the end of the beam that would have occurred if the support was completely fixed. Include a description of the approach you adopted for the analysis of the photographs.

(e) Based on your results in part (d), identify an experimentally-derived orientation for the neutral axis and compare this result with that obtained in part (b) with the aid of a sketch. Discuss possible sources for the differences between the two results.

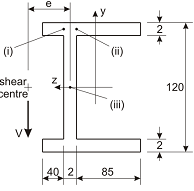
Question 4: Shear stress in beams

Consider the beam section illustrated in the figure to the right. The beam has a shearing force of V = 5 kN acting vertically through the shear centre as illustrated. (a) Determine the shear stress at the three points in the beam, labelled (i), (ii), and (iii). (b) Produce a plot showing the distribution of shear stress across the beam section, noting the shape of the distributions and key values. (c) Determine the distance e (as shown on the figure) which defines the location of the shear centre of this section. (d) With the aid of a sketch, explain the section rotation that will occur if the line of action of the applied shearing force is through the centroid of the section.

2363_Draw a sketch to represent the stress distribution2.png

Reference no: EM13161334

Questions Cloud

What is wrong with her approach and what would you recommend : 1. In C++, operator

State what are the possible values of n3 : Take N3 as the independent variable and solve for N2 in terms of N3. Then solve for N1 in terms of N2 and N3. b. Taking note that there cannot be a negative population, what are the possible values of N3 ?

What is the morphology of the malaria parasite : In what way does malaria affect normal human functioning ie. mcellular respiration, metabolism, e.t.c.?

State potassium phosphate buffer solution : As a technician in a large pharmaceutical research firm, you need to produce 450. of 1.00 potassium phosphate buffer solution of = 7.38. The of is 7.21. You have the following supplies: 2.00 of 1.00 stock solution

Draw a sketch to represent the stress distribution : Calculate the magnitude of the moment acting at the build-in end and specify the orientation of the moment vector relative to the principal centroidal axes of the section with the aid of a sketch and determine the stresses at each corner of the bu..

What are the risk factors for malaria : How do you test for the diagnosis of malaria?

Write a mips program that will alter an array of 100 doubles : Write a MIPS program that will alter an array of 100 doubles. No input or output is required. We will assume somebody else did it. Your program modifies the elements in the array as described

What are the stages of mitosis : what are the stages of mitosis? and how do they differ from meiosis?

Indicate what type of fat substitute you found : Select two sets of products from your daily diet such as butter/ salad dressing and find similar products that use fat substitutes. Make a list of all the fat substitutes that you find listed on the ingredient labels of the products.

User Account

All Pages