Reference no: EM132152286

Question 1 - Answer all parts of this question.

a) A cost accountant has derived the following data on the weekly output of standard size boxes from a factory.

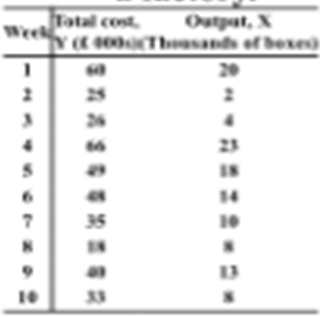
i) Calculate the regression coefficients β^{^}₁ and β^{^}₂ for the equation Y^{^}_i - β^{^}₁+ β^{^}₂X_i before estimating the regression model, plot the data.

ii) Intercept the regression coefficients β^{^}₁ and β^{^}₂.

b) Repeat this question by using log of each of the above variables.

Question 2 - Answer all parts of this question

The following data were given to support the theory that high protein diets reduce the fertility of people:

a) Estimate the least square regression line Y = β₁ + β₂X for the data above.

b) Calculate the coefficient of correlation.

c) Are data o these type adequate to establish a 'cause and effect' relationship between these two variables? Can any conclusions be drawn from the result of your calculations?

Question 3 - Answer all parts of this question

To investigate the relationship between the level of advertising in local papers and the level of sales of a particular consumer product, the marketing manager of a national firm used different levels of advertising in 10 randomly selected geographic areas. The results are given in the table below:

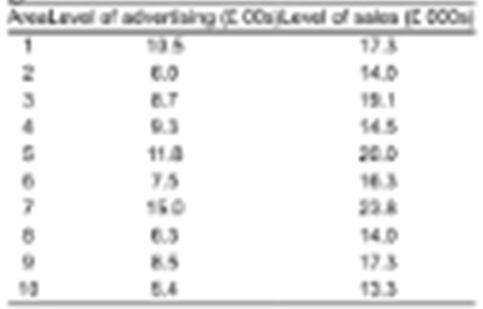
a) Draw a scatter diagram for these data.

b) Estimate the least squares regression line Y = β₁ + β₂X for the data above.

c) Calculate the R² and interpret the result.

d) Use your OLS estimates to predict the level of sales in an area in which £1000 is spent on advertising.