Draw a graph of volume versus time

Reference no: EM132303088

Functions Assignment Questions -

Q1. State whether the following functions are periodic or not.

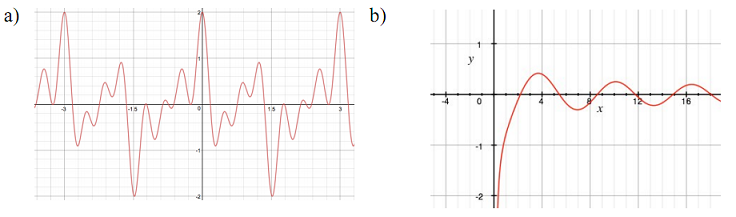
Q2. For each function above that is periodic, state the period and amplitude of the function.

Q3. A periodic function f(x) has a period of 8. The values of f(1), f(5), and f(7) are -3, 2, and 8, respectively. Predict the value of each of the following. If a prediction is not possible, explain why not.

a) f(9)

b) f(29)

c) f(63)

d) f(40)

Q4. Sketch the graph of a periodic function with an amplitude of 8 and a period of 5. Explain why your function is periodic.

Q5. Sketch the following graphs:

a) y = 3 sin[2(x - 30^o)] - 2

b) y = -2 cos[½(x + 45^o)] + 1

Q6. Let f(x) = 3 cos[3(x - 37^o)] + 5. State the amplitude, period, phase shift, and equation of the axis.

Q7. Write an equation for the sine function with the following characteristics:

Amplitude: 5

Period: 90^o

Phase Shift: 72^o to the left

Equation of the Axis: y = -9

Q8. Write the equation of the following function:

Q9. The volume of air in the lungs during normal breathing can be modelled by a sinusoidal function of time. Suppose a person's lungs contain from 2200mL to 2800mL of air during normal breathing. Suppose a normal breath takes 4 seconds, and that t = 0s corresponds to a minimum volume.

a) Let V represent the volume of air in a person's lungs. Draw a graph of volume versus time for 20 seconds.

b) Write an equation of a sinusoidal function to represent this relation.

c) Describe how the graph would change if the person breathes more rapidly. Explain your answer.

d) Describe how the graph would change if the person took bigger breaths. Explain your answer.

Reference no: EM132303088

Questions Cloud

Predicting a missing data point using data : Topic - How to Predict an Outcome (Simple Linear Regression) - Predicting a missing data point using data from the Cognitive Failures study

Explain why the operational losses cannot be broadly managed : Explain why the operational losses cannot be broadly managed. Why do they have to be categorized? For each operational risk exposure listed below, provide.

Key elements of web analytics : MBA 640 - Innovation Through Marketing and Technology - University of Maryland University College - Review the readings, participate in the discussion activity

How many winners are there in total explain : In a lottery, the owner of the first ticket drawn receives $10000. How many winners are there in total? Explain

Draw a graph of volume versus time : MCR 3U Functions Assignment Questions - Let V represent the volume of air in a person's lungs. Draw a graph of volume versus time for 20 seconds

Why vaccinations necessary components of healthcare programs : Why are vaccinations necessary components of the healthcare programs? Are there reasons for people not being vaccinated despite of such elaborate healthcare.

Discuss about a health issue in a specific population : Research and read about a health issue in a specific population in specific regions in the United States. Some examples of the topics for your research could.

What is the general effect of dehydration on the body : Write an essay of at least 350 words that explains the basic functions and sources of minerals and water in the body. Include what you learned about mineral.

How can an entrepreneur keep entrepreneurial ego in check : Name three traits of successful entrepreneurs and explain in detail why they are important qualities for an entrepreneur to possess.

User Account

All Pages