Reference no: EM133076410
DSC-550 Neural Networks and Deep Learning - Grand Canyon University
Project: In this assignment, the learning rule for perceptron is examined as an example of proper network behavior. The notions of gradient descent and stochastic gradient descent are emphasized, as well as post-training and the implication of fitting a model to a training data set. Overfitting is addressed and the tradeoff of bias as compared to variance is also discussed.
Consider a single-neuron perceptron with a hard limit transfer function (hardlim).
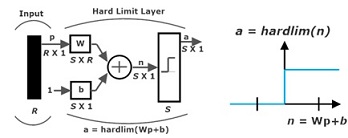
The hardlim transfer function is defined as:
a = hardlim (n) = { 1 if n ≥ 0; 0 otherwise }
Using the single-neuron perceptron, solve the three simple classification problems (a), (b), and (c), shown in the figure below:
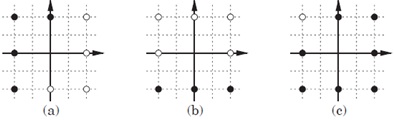
1. Draw a decision boundary.
2. Find the weight and bias values that result in a single-neuron perceptron with the chosen decision boundaries. Observe the fitting model data to a training data set.
3. How would you find the variance for this problem case?
4. Check your solution (post-training data) against the original points.
5. Use Python and the corresponding libraries to automate the testing process, and to try new points.
Attachment:- Neural Networks and Deep Learning.rar