Reference no: EM13960551

Electrical Power and Drive Systems

Problem 1. A 3-phase power system is represented by the single-line diagram shown in Figure Ql. The per unit (pu) positive, negative and zero-sequence reactances shown are all to a common 100 MVA base.

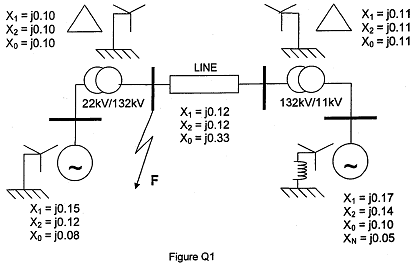
a) Assuming that the synchronous generators remain at their rated voltages, calculate the fault current and fault level for each of the following zero-resistance short circuits at point F in Figure Q:

(i) single line-to-ground,
(ii) line-to-line

Comment on the difference in fault levels for these two types of fault.

b) Calculate also the voltage of the 'healthy' line in case (ii) above.

c) Explain briefly how the solutions to parts (i) and (ii) above will be affected if the fault at point F has an impedance ZF.

Problem  2. (a)

(i) Explain briefly why an iterative numerical technique is required in load-flow studies of power systems.

(ii) State the general form of nodal voltage equations for a network and derive expressions for the voltage and input reactive power at any node in the network.

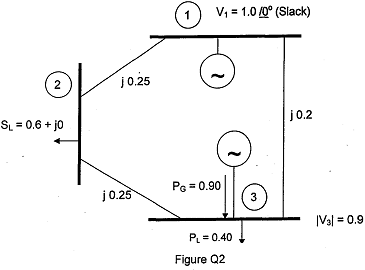
(b) The single line diagram of a three-phase power system is shown in Figure Q2. The data for voltages, generation, loads and reactance are all in per unit (pu) to the same MVA base. Using the Gauss-Seidel iterative method, stating any assumptions made, find each of the following after the first iteration:

i) The voltage at busbar

ii) The reactive power Q₃ and the voltage angle δ₃ at busbar

iii) Explain clearly and concisely how the Gauss-Seidel method should proceed to its conclusion.

Problem 3. (a) Compare the effects of internal and external events in the generation of over-voltage transients in h.v. power systems. Explain the relevance of these effects to the specification and protection of plant.

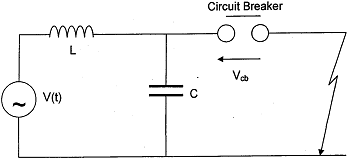
(b) Figure Q3 is the single-phase representation of a 3-phase, 50-Hz, power system with negligible resistance. A symmetrical short circuit to earth occurs on the system immediately beyond the circuit breaker.

i) Derive an expression for the voltage across the circuit breaker contacts, V_cb(t), immediately after current interruption if this occurs at a current to prior to natural current zero. You may assume that the supply voltage remains constant at its maximum value, Vm, during the fault and that the arc voltage across the circuit breaker contacts prior to current interruption is negligible.

ii) Given that system voltage V_L = 15kV, L = 10mH, C = 4pF and the interruption occurs 11° prior to current zero, show that the voltage V_cb(t) in kV is given by:

V_cb(t) = 12.25(1 - Cos (5000t) 37.22Sin (5000t)

iii) Hence estimate a value for the 'Rate of Rise of the Restriking Voltage' (RRRV), and briefly explain the practical significance of and the factors influencing RRRV.

Problem 4. a) Using a half-wave, three-phase, controlled rectifier bridge as an example, explain the phenomenon and effects of 'overlap'. Draw circuit and waveform diagrams as necessary to illustrate your answer.

Derive an expression, in terms of the supply voltage, for the voltage presented to the load during the overlap period.

b) For a p-pulse, controlled rectifier bridge, without flywheel diode, the average dc voltage presented to the load, is given by:

V_dc = P√2V_s/Π.Sin(Π/P)cosα - PωLIL/2Π

Where

V_s = the supply voltage

I_L = the line current

L = the source inductance (per phase)

P = the number of pulses per cycle

α = the delay angle beyond the natural commutation point

It is required to provide variable speed control of a 300 V, separately excited, dc motor using a 6-pulse converter. The motor armature current rating is 600A, its speed rating is 1500 rpm and the armature resistance is 30.0 mQ.

The supply frequency is 50 Hz and the source impedance is j0.09 CI per phase.

i) Calculate the minimum line voltage required to operate the motor at its rating with the above arrangement.

ii) Determine the value of a when the motor is operated at 1000 rpm at one third rated torque with a supply voltage V_L = 300 V.

Problem 5. a) Draw a circuit diagram plus voltage and current waveforms, to illustrate how the speed of a permanent magnet dc motor may be controlled from a dc supply using a chopper drive.

b) A single-phase, half-controlled full-wave bridge rectifier supplies dc to the armature of a separately excited dc motor. The rectifier is supplied from a 220 V, 50 Hz, single phase supply. The bridge is fired at an angle of 110^o and the current in the armature lasts for 110° in each cycle. The motor has an armature resistance of 0.6 Ω and a motor Constant of 0.97 Nm/A. Neglecting rectifier device and overlap volt drops, if the motor emf is 80 V determine:

i) the speed of the motor in rpm,

ii) the average armature voltage, and

iii) average armature current.

Problem 6.

a) Induction motors may present an operator with difficulties when they are connected to a 'weak' supply and are required to start against load. Explain how a Variable Speed Drive (VSD) can provide a better solution than other 'soft-start' methods.

b) A three-phase induction motor is to be used to pump cooling water in an industrial process. It is required to vary the flow rate between 1.0 and 0.4 per unit (pu) and flow rates across this range of values are equally probable over time.

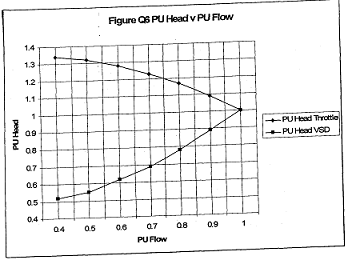
Flow rate can be varied by throttling or by using a VSD. Figure Q6 shows the relationship between pu Head and pu Flow for both methods
At a flow rate of 1 pu the mechanical output power is 4 kW and there are system losses of 0.25 pu comprising:

0.075 pu fixed losses

0.075 pu Torque squared losses 0.1 pu Speed squared losses

Estimate the time taken for the VSD to pay for itself given that electricity costs are 9p per kWh and the cost of installing the VSD is £1000 more than that of the throttling system.

You may assume that:

1 Torque is proportional to Head for both methods.

2 Speed is proportional to Flow for the VSD system and fixed for the throttled system.

Attachment:- Exam.pdf