Reference no: EM13999

1. The following is a very simple, discrete-time model for an economy. This model consists of four risky assets, A, B, C and D, and nothing else. We denote their prices at time t by At, Bt, Ct and Dt, respectively. The values of these assets now, at time t = 0, are

A₀ = $11; B₀ = $5; C₀ = $15; D₀ = $8:

The assets are risky because in the future, at time t = 1, there are three possible states of the world, !1, !2 and !3, which occur with probabilities p1 = 1=2, p2 = 1=3 and p3 = 1=6, respectively, and the values of assets at time t = 1 vary according to which state of the world occurs; in the rst state, !1, the values of the assets at t = 1 are

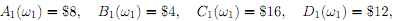
while in the second and third states, ω₂, and ω₃, they are

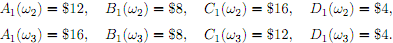
i) Show that in this model it is possible to set up a portfolio now (at time t = 0) consisting of  units of asset A,  units of asset B, units of asset C and units of asset D in such a way that if the composition of the portfolio remains fixed then the value of the portfolio at t = 1 is guaranteed to be $40 (i.e., its value at time t = 1 is $40 regardless of which of !1, !2 or !3 actually happens).

Assume that it is possible to own, buy or sell a fraction of an asset but that it is not possible to sell something you don't own, so that , ,
and  need not be integers but they must be non-negative. Find a particular set of values of , ,

and  and the corresponding cost (at time t = 0) of setting up the portfolio.

What is the prota (or loss) on this portfolio?

ii) Show that there are, in fact, an innite number of such portfolios and that the costs of setting them up (at time t = 0) are not all equal. What is the maximum prot you can make on a single portfolio given that it is guaranteed to have a value of $40 at time t = 1?

iii) If we relax the assumption that you can't sell something you don't own, what is the maximum prot you can make on such a portfolio?

Probability

3. A treasure chest containing N gold coins has been found by a group of pirates. The pirates form a queue and look into the treasure chest one by one. When a pirate nds k  1 coins in the treasure chest, he (or she) takes a random number of coins that is uniformly distributed on f1; 2; : : : ; kg.

i) Compute the expectation of the number of coins taken by the second pirate, as a function of the initial number of coins N.

ii) For n 2 N, let Sn denote the sum

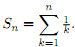
Prove that the following equality holds for all nεN.

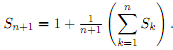
iii) Let EN denote the expected number of pirates who take at least one coin from the treasure chest given that it initially contained N coins. Derive a formula that represents EN+1 in terms of E1 +......+ EN. Then using part ii) (or otherwise) express EN in terms of N.

4. For k; θ > 0, the Gamma(k; ) distribution is dened by the following density function

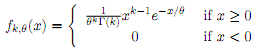
where the function : (0;1] ! R is dened as follows.

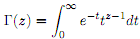
i) Let X  Gamma(k1; ) and Y  Gamma(k2; ) be independent random variables for some k1; k2;  > 0. Show that (X + Y )  Gamma(k1 + k2; ). [You may assume without proof that

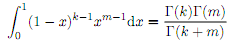
for k;m > 0.]

ii) Derive the distribution of Pn i=1 Xi where Xi  Gamma(ki; ) for i = 1; : : : ; n are independent random variables for some k1; : : : ; kn;  > 0.

iii) For  > 0 and n = 1; 2; : : : , let the random variable Zn be dened as

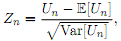
where Un  Gamma(n; ).

Using part i), part ii) and the Central Limit Theorem (or otherwise) show that Zn converges in distribution as n →1. Specify the limiting distribution. [You may assume without proof that the Gamma(k; ) distribution has nite rst and second moments for k;  > 0.]