Reference no: EM133685554

Theory of Computation

Question 1

Let Σ = {a, b}. Construct a DFA for the language {w | w has an odd number of a's}. You can either give the formal definition of the DFA or draw a state diagram of the DFA.

Let Σ = {0, 1}. Give regular expressions generating the following language, {w| every odd position of w is a 1}

CFG G is given below:
S→RT
R→TR|a
T→TR|b

Does G accept string w=baba? If so, show the derivation tree.

Are 7289 and 8029 relatively prime? Show the calculations that led to your conclusions.

Question 2: Prove the language {0^m1ⁿ | m≠n} is not regular.

Question 3: Answer the following questions:

What is the difference between Turing Recognizable and Turning Decidable? Could you give a language which is Turing recognizable and not Turing decidable?

What is the relation between P, NP and NP-Complete? Could you find a language which belongs to the class of NP but not belong to class of P?

Are all languages Turing Recognizable? Briefly explain your answer.

Question 4: Categorize the following languages:
B = {aⁿbⁿcⁿ | n 0}.
SAT (satisfiability) problem.
Hamilton path problem.
HALT problem.
Co-HALT problem.
Turning-recognizable language(s):
Turning-unrecognizable language(s):
Turning-recognizable but undecidable language(s):
Class P problem(s):
NP-completeness problem(s):

Question 5: A triangle in an undirected graph is a 3-clique. Show that TRIANGLE?P, where TRIANGLE={ <G> | G contains a triangle}.
(Hint: you need to design an algorithm to tell if an undirected graph contains a triangle in polynomial time.)

Question 6: Given a graph G = (V, E), a vertex cover in G is a subset V' V such that for all (u,w) E, u V' or w V'.

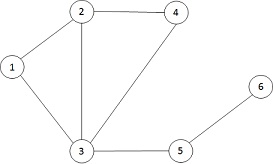
Figure 1

Figure 1 shows an undirected graph including 6 nodes. Answer the questions below:

• Does Figure 1 have a vertex cover including four nodes? If so, given an example of 4-node vertex cover?
• Does Figure 1 have a vertex cover including three nodes? If so, given an example of 3-node vertex cover?
• What is the minimum vertex cover (including least nodes) in Figure 1?
• Let VC = {<G, k> | G has a VC of size ≤ k}. Is this problem a NP problem? Prove your conclusion.
• Is VC a NP-complete problem? Why?