Reference no: EM13983589

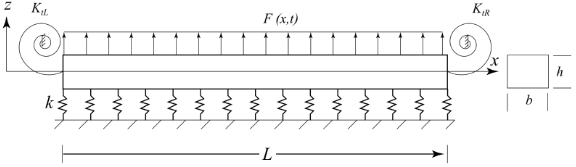
Figure 1. Forced beam with elastic foundation and torsional springs at each end.

Given: the beam shown in Figure 1, with density, ρ, kg/m³, and Young's modulus, Y N/m². It is supported by an elastic foundation of linear stiffness, k N/m², and by torsional springs at each end of torsional stiffness K_tL, and K_tR N-m/rad., respectively. Assuming pure bending - i.e. zero membrane resultants and resultant strain, so that the strain in the beam is determined by the Euler-Bernoulli assumptions

ε_x = z∂²u/dx²                           (1)

where z is measured from the mid-plane of the beam:

1. Derive an expression for the kinetic energy - i.e. show that kinetic energy is given by

T = 1/2 ρbh ₀∫^L(∂u/∂t)²dx                      (2)

2. Derive an expression for the potential energy due to bending - i.e. show that the bending potential energy is given by

V = 1/2 YI ₀∫^L(∂²u/∂x²)²dx           (3)

where Y denotes the Young's modulus, and I = 1/12bh³

3. Develop an expression for the potential energy due to the elastic foundation of linear stiffness, k.

4. Develop expressions for the potential energy contributed by the torsional springs.

5. Develop an expression for the virtual work done by the distributed force, F(x, t).

6. Apply Hamilton's principle to determine the equation of motion.

7. What are the possible boundary conditions? What are the admissible (which apply the the current case) boundary conditions?