Reference no: EM133123938
Modelling for Decision Science Coursework
Exercise 1:
The Verhulst model for population growth that includes self-limiting process that control the population getting too large, is described by the equation
dN/dt = rN(1-N/K)
a) Describe what r and K represent in equation (1) giving their units and brief biological description (1).
b) Find the steady states of the Verhulst model. By linearising around the steady states, show that one of the steady states is always unstable while the other one is always stable.
c) Setting the initial population to be NO, show that the general solution of equation (1) that describes the population N at time t is
N(t) = N0Kert/K+N0(ert-1)
Find the limit of N(t) as t → ∞ and state how this is related to the steady states you found in (b).
d) Sketch the solution N(t) over time and discuss how the shape of N(t) differs in the following cases
(i) N0 < K and N0 > K
(ii) N0 < K/2 and K > N0 > K/2
Exercise 2 - Infectious diseases modelling
A new infectious disease caused by a bacterium is known is to be transmitted via person-to- person contact. Currently, the 10,000,000 inhabitants of an island are susceptible to this bacterial infection. However, on day T=0, 500 previously infected individuals travel to the island, becoming infectious the moment they land. We assume that once an individual is infected they become infectious after 7 days. In the absence of treatment, individuals remain infectious over a period of 14 days, following which they recover and enter a period of temporary immunity to infection, which is lost after 3 months.
Using the information above, develop a mathematical model describing the transmission dynamics of this infectious disease, parametrise the model, and discuss your results. In your model we ask you to define your time step and assume that the model is run over a period of one year. Specifically:
Sketch a compartmental model diagram that shows the disease states characterising the transmission of this infection. Denote movements between compartments with arrows and add the rates at which individuals move between these compartments. Describe this model by defining compartments and parameters.
Based on the law of mass action, write the differential equations that describe the change over time in the size of the different compartments, what are the values of the parameters you defined in 2.1?
Numerically solve the system of equations from 2.2 in MATLAB and copy the code into your coursework document. Generate temporal profiles for the cohorts of susceptible and infectious individuals in two different scenarios by modifying the transmission rate, discussing the differences between the two solutions.
Add births and natural deaths (B=1000 and µ=0.0002) to the equations from 2.2 and study the stability of this model. Specifically:
(i) describe all the steps needed to study the stability of a system,
(ii) study the stability of this system using MATLAB and copy the code into your coursework document, and
(iii) following the parametrisation used to identify one of the temporal profiles in 2.3 with the additional demographics parameters here defined (B=1000 and µ=0.0002), identify the equilibria points and their type and justify your answer.
Exercise 3 - Linear regression
Part 1
Consider the following set of observations (x; y) = (independent variable; dependent variable):
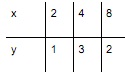
Apply linear regression analysis to find a horizonal line that best fits the observed data:
i. Write the hypothesised model structure.
ii. Write the normal equations in matrix form.
iii. Solve the normal equations to determine the unknown model parameter.
iv. Draw a plot representing the observed data and the fitted curve, clearly labelling it.
Part 2
Your client is planning to conduct school-based flu vaccinations. For a vaccination session, a class is brought to the vaccination room, the children are administered the vaccine and then they are taken back to their classroom. Your client asks you to predict the relationship between the class size (independent variable) and the time needed to vaccinate a class (dependent variable). They have collected the following dataset during a pilot campaign:
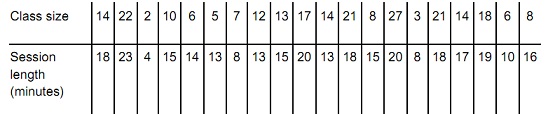
You have decided to compare the following two model structures to predict the value of y based on new observations of x:
v. Describe how you would use the above dataset to set up a machine learning approach based on linear regression to decide which of the two models above should be used by your client.
vi. Using MATLAB, solve the above problem. Report the code you used and your results using tables or plots as appropriate.
vii. Which of the two models should your client use and why?
Exercise 4
1. Identify whether the examples below correspond to supervised, unsupervised or reinforced learning
a. An algorithm that classifies customer preferences by tracking the websites they visit.
b. Trying to predict the weather using historical data of temperature, humidity and precipitation.
c. A programme that identifies the most important variables, or features, that will determine if a patient has a medical condition or not.
d. Detecting automatically whether an X-ray image corresponds to a certain class of tumour.
e. Forecasting the price of houses next year based on historical data.
f. Creating a programme that learns how to play a certain video game.
2. Load the fisheriris data set in Matlab. Convert it to a table with variables SepalLength, SepalWidth, PetalLength and PetalWidth. Write the code to perform the following analyses:
a. Plot a matrix of subplots with 1 row and 4 columns, each corresponding to the histograms of the data table. Don't forget to add the corresponding title to identify each subplot.
b. To each one of the subplots, add 3 vertical lines corresponding to the distribution's 5-th, 50-th and 95-th percentiles. Use the Matlab help, or look online for how to calculate the percentiles. The lines corresponding to the 5-th and 95-th percentiles should be red and dotted, the line corresponding to the 50-th percentile should be black and solid.
c. Build a random forest with 39 trees. The Out of Bag prediction should be off, the sampling with replacement should be on, and the forest should be constituted by classification trees.
d. Use the code below to generate 40 random points. Then, code up the k-means algorithm using 4 centroids and plot them. The colours of the clusters should be: red, blue, green and magenta. The centroids should be black. Use any marker shape you prefer.
rng(1)
X = [randn(40,2)+ones(40,2); randn(40,2)-ones(40,2)];
e. Report the coordinates of the centroids (to 2 decimal places).