Reference no: EM13522980

Your paper can be either an investigation or a survey. If the former, your paper should present an interesting problem or technique relating to object orientation. It should state the problem, provide background and motivation, and describe novel approaches (proposed by others or by you). Your paper might or might not require programming, depending on its focus. Alternatively, if you write a survey, it should be based on key papers related to the area you choose. Regardless of whether your paper is an investigation or a survey, it should include key references and should run about 12-16 double-spaced pages in length.

In addition to the resources cited in the bibliography section of our course syllabus, use NSU's online databases, particularly the ACM Digital Library, IEEE Computer Society Digital Library, and ScienceDirect.

Programming project

Develop an interesting program in Ruby. Possible projects:

- Significantly enhance one of the programming assignments from this course.

- Develop a game, such as a board, adventure, word, or computer game.

- Develop a domain-specific language (DSL) within Ruby, such as for manipulating files in a directory system, editing files, generating quizzes, describing graphical or geographical scenes, and adding and viewing entries in a calendar.

- Develop useful metaprogramming tools, similar to the attr_* class methods, or the methods defined in the Forwardable or Singleton modules.

Elevator project

Develop a simulation of an elevator that travels between floors 1 and N where N is an input. Time is sequenced in discrete steps starting at 1; at each time step, the elevator may ascend one floor, descend one floor, or remain at its current floor, as determined by its strategy. The first line of the input file indicates the number N of floors. This is followed by one line per person using the elevator: her id, call time (when she calls for the elevator), origin floor (where she boards the elevator), and destination floor (where she debarks the elevator). For example:

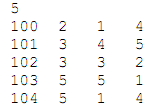
Here, individual 100 boards at time 2 from floor 1 with a destination of floor 4. Assume sensible inputs (e.g., times are positive integers, floors are integers in the range 1 through N).

Whenever the elevator stops at a floor from which people have called it (i.e., their origin floor but not before their call time), they all board the elevator. And whenever the elevator stops at any passengers' destination floor, they all get off the elevator. (Everyone behaves so as to minimize their travel time.) The simulation stops when every individual has been brought to their destination floor (subject of course to their call time and origin floor constraints).

A strategy determines the floor the elevator begins on at time 1, and a policy for moving to the next floor (up one floor, down one floor, or remaining at the current floor) from one time step to the next. Here is a simple strategy:

Strategy 1: Start at floor 1. In each time step, successively go up one floor until reaching the top floor N, then successively go down one floor until reaching the bottom floor 1, and continue this ‘up to the top floor then down to the bottom floor' policy.

We measure the efficiency of a strategy with respect to the passengers' average wait time. Let's say that someone's wait time is the number of time steps from her call time until she reaches her destination floor. So wait time is the time waiting for the elevator to arrive at the origin floor plus the time traveling in the elevator to the destination floor. For example, the wait times for customers 100 through 104 are 10, 2, 5, 4, and 7, respectively. Then we define the efficiency of a strategy (with respect to input) to be the average wait time over all customers. Our simulation reports this value for the simulation just run:

>> puts sim.average_wait_time
5.6

Here is what you need to submit:

1. A scenario diagram for the case where a customer calls the elevator, the elevator arrives, she boards, the elevator moves (over time) to her destination floor, and she debarks. You may devise other diagrams but this one is essential. You are welcome to discuss and work on your design on our discussion board and during class time (but you should implement the project on your own).

2. Implement Strategy 1 as part of your project. In addition, devise and implement a second strategy that is generally more efficient than Strategy 1. Where sim is a Simulation object, we run a simulation like this:

sim.run(filename_string, strategy_symbol)

The symbol :strategy2 should identify your (more efficient) strategy.

3. Write a method

sim.multirun(nbr_runs, filename_prefix, strategy)

that runs your program nbr_runs many times on the input files named by filename_prefix with suffixes 000.in, 001.in, ..., and returns the average efficiency. For example:

sim.multirun(15, 'myelev', :strategy2)

runs your Strategy 2 on the files myelev000.in, ..., myelev014.in and returns the average of the 15 efficiency values. I will give you a set of input files to test your program on, and you should report the average efficiency you obtain on these files for both strategies. You can also use these input files to compare your strategy to other strategies, with respect to efficiency. I'll also give you a short Ruby program to generate your own test files.

4. Submit your Ruby code for this project, in addition to your scenario diagram, in a zip archive by the due date.

An opportunity for discussion and presentation of projects toward the end of the term. We have too large a class to allow everyone to give a presentation, but those of you who wish to give one.