Reference no: EM132846772

Question 1. Given below is a network of roads connecting cities, namely A, B, C, D, ...... up to N. Among these cities, F, L, H, and M are islands.

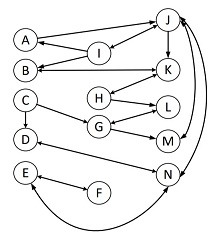
Answer the following questions based on the network (build the adjacency matrix and solve):

(i) Which city(s) has/have the highest inbound road connections?

(ii) Which city(s) has/have the highest outbound road connections?

(iii) Which city(s) has/have the lowest inbound road connections?

(iv) City J has the highest density of road connections; which is second?

During the recent Maroon-19 epidemic, the government wants to isolate the infected persons and relocate them to the islands. Eventually, all road connections to and from these islands will be closed for future precautions.

Note: When you calculate the density for the revised network, make sure to count only those nodes among whom connections are possible!
Answer the following questions based on the revised network:
(v) More than one city has the highest inbound roads. The top two cities are?
(vi) Which city(s) has/have no road connections at all?
(vii) More than one city has the highest density of all roads. The top two cities are?

Question 2. Sean Murphy is the IT Manager of the Boston store for Best Cost Retail, a USD 21 billion retail chain across North America. She needs to replenish her supply of blueberries every day. Her regular supplier can provide as many cases as required. However, because these blueberries are already very ripe, she will need to sell them tomorrow and then discard any unsold. Sean estimates that she will be able to sell 10. 11 12, 13, 14, 15, 16. or 17 cases tomorrow. She can purchase the blueberries for $3.50 per case and sell them for $8.50 per case. Sean now needs to decide how many cases to purchase.

Sean has checked the store's records on daily sales of blueberries. On this basis, she estimates that the prior probabilities are 0.150, 0.125, 0.133, 0.115, 0.100, 0.133, 0.125. and 0.120 to sell 10, 11, 12, 13, 14, 15, 16, and 17 cases of blueberries next day.

Answer the following questions based on the above information:

(i) Develop a decision analysis formulation of this problem by identifying the alternatives and the states of nature. Subsequently, build the payoff matrix.

(ii) How many cases of blueberries using the maxi-max payoff criterion?

(iii) How many cases of blueberries using the mini-max payoff criterion with regret?

(iv) How many cases of blueberries using optimistic criterion with alpha = 0.35?

(v) Sean thinks she has the prior probabilities just about right for selling 10, 12, 14 and 16 cases, while the prior probability for selling 17 cases is 0.0125. However, she is uncertain about the probabilities for 11, 13 and 15 cases and they could be equally likely. Apply the expected payoff rule and decide how many cases of blueberries Sean needs to purchase?

Question 3. Apply the IT Governance Assessment Matrix (shown below) proposed by Weill and Ross (2004) to examine the enterprise-wide IT Governance at DuPont Chemicals (Case Study attached).

I = Inputs to Decision: D = Decision-Making