Reference no: EM1380284
Problem 1. Consider a steel cantilever beam with length of l = 18 ft under a distributed random dead load. Furthermore, assume that yield stress and section modulus S are also random variables. All the random variables are uncorrelated with the following information.
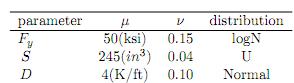
1. Estimate reliability in terms of bending stress with 500, 1000, and 10000 samples. Summarize the results in a table.
2. Plot the empirical pdf for all of your generated random numbers. Evaluate the mean and standard deviation from your generated data, and compare to the requested values in a table.
Comment on the pdf 's, do they look reasonable to you?
3. Plot the dead load data on a normal probability paper using our previous functions.
4. Compare your results with FOSM method (bonus:5 pts ).
Note. The demand is expressed as M S , where M is the moment due to the load at the �xed end.
Problem 2. We would like to write a MATLAB function to generate random numbers from Extreme type I (Gumbel) distribution. The CDF is given as FX(x) = e-e-(z-1)/s, with parameters of l (location) and s (scale). The quantile function (inverse cumulative distribution function), Q(p), of a Gumbel distribution is given by
Q(p) = 1 - sln(-ln(p))
the variate Q(U) has a Gumbel distribution with parameters l (location)and s (scale) when the random variate U is drawn from the uniform distribution on the interval (0; 1). Therefore, this simply means that your function should �rst call the rand function of MATLAB to generate U. It will then use the above formula to transform into Gumbel (Recall the equation
on the last page of handout 4). The function should get three things as input: number of data n, l and s the parameters of the requested Gumbel distribution. It should then, as an output, return a vector of numbers.
Problem 3. Consider the following performance function for bending of a rectangular reinforced concrete beam under moments due to dead and live loads.
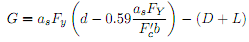
where the deterministic dimensions and rebar area are given as follows: b = 15 in, d = 24 in and a = 5 in2. The random variables are assumed to be uncorrelated with the following information.
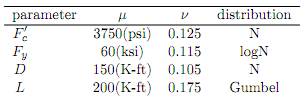
Estimate probability of failure with Monte Carlo simulation using 500; 1000; 10000 samples. Summarize the results in a table. What would your �nal answer be?
|
Question related to normalization
: Think about a typical job order that might include the following information. Design a single table to hold all the data needed to store a job order including this information.
|
|
Create a context level dfd
: Create a context level DFD. You should take your DFD to your tutorial for feedback before starting on the ER.
|
|
Entity relationship diagrams
: Discuss why are Entity Relationship Diagrams an important initial stage in developing databases? Who would be the initial parties interacting to develop the ERDs?
|
|
Question about database structure
: Determine when a typical database is created the structure is constructed before the data is actually loaded into the database. What problems exist when someone wishes to add or delete from the existing structure?
|
|
Deterministic dimensions and rebar area
: Performance function for bending of a rectangular reinforced concrete beam under moments due to dead and live loads
|
|
Documentation and proper design procedures
: Determine the main reason that make many developers skip over the documentation and proper design process? As a manager, discuss how do you ensure that the proper database design process are followed by database development teams?
|
|
Clerical office placement setting
: Determine what other databases would be known to benefit a clerical or job placement organization using databases?
|
|
Question about damaged database
: Suppose if you were one of the users of a damaged database, discuss how would you be affected by such a failure and what measures could you take to prevent it?
|
|
Implementing one to one relationships
: Explain the different ways of implementing one to one relationships. Suppose you are maintaining information on offices and faculty.
|