Reference no: EM13797146
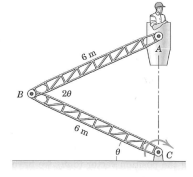
Q.1 In order to transport the worker vertically, the mechanism ABC is designed such that the angle ABC (2θ) is always twice the angle between BC and the horizontal (i.e. θ). Determine the angular velocity θ & (in rad/s) required to raise the worker at a velocity of 0.5 m/s when θ = 30°.
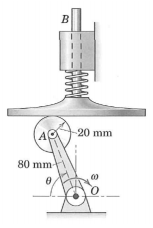
Q.2 Determine the velocity and acceleration of the shaft B when the angle θ is 50° and the angular velocity ω of OA is 4.0 rad/s (clockwise) and the angular acceleration of OA is zero. The spring is there to ensure that contact with the roller is maintained.
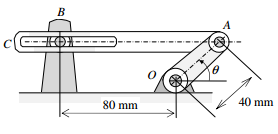
Q.3 In the mechanism shown, when θ = 45 °, the component AC is horizontal. Determine the angular velocity of the rigid body AC when θ is 45° and θ & is 2.0 rad/s.
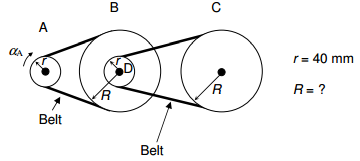
Q.4 In the V-belt speed-reduction drive system shown pulley A starts from rest with a constant angular acceleration of αA = 0.2 rad/s2 for 20 s. Pulley D is rigidly attached to pulley B. Starting from rest, pulley C is required to do a total of 1 revolution in 20 s. Determine the required radius R of the larger pulleys.
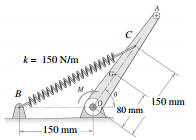
Q.5 The member OA has a radius of gyration of 95 mm about O and a mass of 0.4 kg. The spring BC has an unstretched length of 100 mm. Starting from rest with an angle of θ = 90° a constant moment M = 10 N.m is applied until θ = 60°. Determine the magnitude of the velocity of point A when θ = 60°. You may neglect friction.
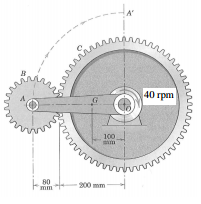
Q.6 In the gear assembly shown below, the larger gear C is rotating clockwise with a constant angular speed of 40 revolutions per minute. The link OA starts from rest at the position shown and rotates through 90° to the position OA′ in 0.5 seconds. Assuming a constant angular acceleration for the link OA, determine the angular velocity of the gear B when its center is at A′. Is gear B rotating in the clockwise or anticlockwise position?