Determine the vector product of each set of vectors

Reference no: EM13803171

1) Given three vectors F₁ = 35, F₂ = 40, F₃ = 80 (see the diagram for the angles), find the resultant vector of all three using the component method.

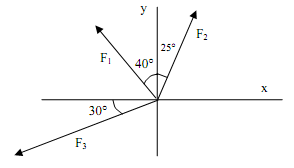
2372_Determine the vector product of each set of vectors.png

2) Repeat Problem #1 using unit vectors. Make sure you write out each vector using unit vectors first and show ALL of your work.

3) Using the vectors F₁ and F₂ from Problem #1, find the following, leaving your answers in unit vector notation.

a) F₁ - F₂

b) 2F₂ - F₁

c) F₁ + F₂

d) F₂F₁

e) F₂ (F₁ + F₂) / F₁

4) For the vector A = - 8j + 4k, find its magnitude and direction. Also state in what plane the vector resides.

5) Given the vector: A = 3i + 4j, find any three vectors B that also lie in the xy plane and have the property that A = B but A ≠ B. Write out these vectors with unit vector notation.

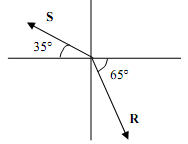
6) Given two vectors; S = 2.5, R = 4.2, (see the diagram for the angles), find the dot product using (a) the magnitudes and (b) unit vector notation.

858_Determine the vector product of each set of vectors1.png

7) Calculate the angle between the two vectors given by:

b = 3i - 2j - 8k , c = i - 5j + 4k.

8) Determine if the following vectors are perpendicular to each other.

a) P = 3i - 2j + k , Q = 4i + 9j + 6k.

b) D = i + 2j - 5k , F = 2i - 7j + k.

9) Determine the vector product of each set of vectors.

a) P = 3i - 2j + k , Q = 4i + 9j + 6k.
b) D= i + 2j - 5k , F = 2i - 7j + k.

Reference no: EM13803171

Questions Cloud

Describe the business : Explain the organization’s mission and vision statements to address the direction of the business.

Write a paper about stories- on excellence and spare change : Write a paper about the following stories- "On Excellence", "Spare Change" and "Call Me Crazy, But I Have to Be Myself".

Most recent annual reporting period : a. What were the company's total current assets at the end of its most recent annual reporting period? b. What were the company's total current assets at the end of the previous annual reporting period?

Write a paper on the novel the octopus by frank norris : write a 5-7 page paper on Frank Norris's novel The Octopus. You may choose from one of the approaches below. Please limit yourself to ONE of the approaches.

Determine the vector product of each set of vectors : Calculate the angle between the two vectors - Determine the vector product of each set of vectors.

Describing demonstrative communication : Write a 700- to 1,050-word paper describing demonstrative communication. Demonstrative communication includes nonverbal and unwritten communication and involves such things as facial expressions, tone of voice, body language, and so forth. Include..

Correlation between ceo salaries : Do you think there is a correlation between CEO salaries and the degree of success of a company?

Campaign and electoral reform : Campaign and Electoral Reform

Epidermis and dermal layers of skin : ermis and dermal layers of skin. What is the significance of each of these layers? For example, consider permanence and scarring.

User Account

All Pages