Reference no: EM132585101

QUESTION 1

Part 1
Please enter your Student ID number in the box below to confirm that you have read, understood and will abide by the University statement on cheating and plagiarism included in the University's Code of Practice on Student Discipline (Academic), and that the answers you submit to this online test will be your own or, where the intellectual work of others is used, it is clearly identified and referenced.

The School of Engineering reserves the right to use this submitted work in the detection of plagiarism.

Please note that this question is worth zero marks, but must be completed.

Part 2
Consider a generic closed-loop feedback control system, whose block diagram is shown in the figure below. This diagram will be used in follow-up questions, where it will be referred to as Figure 1.

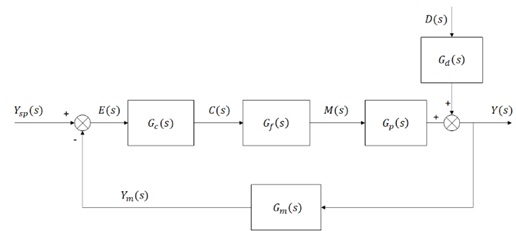
QUESTION 2

For this question consider the system shown in Figure 1. Furthermore, assume the following about its transfer functions:
• Controller: Proportional-Derivative with derivative time constant equal to 1.48 min.
• Final control element: First order lag with a gain of 1 and a time constant of 0.135 min.
• Process: Second order with a gain of 1, a natural period of oscillation of 0.22 min and a damping factor of 0.06.
• Measuring device: First order lag with a gain of 1 and a time constant of 0.58 min.
• Disturbance: Same as the process with a gain half of that of the process.
Based on the above data, and applying the 7 rules for Root-Locus definition, give answers to the questions below. Even though it will not be requested from you to upload a picture file of the final diagram, it is advised that you construct the Root-Locus of this closed-loop control system and consult it when answering the questions below.

1.Determine the number of poles, n, the number of zeros, m, and the number of branches in the Root Locus that terminate at infinity, n-m. The answer should be provided in the format "n m n-m", so for example "3 1 2":

2.Determine the intervals on the Real axis that belong to the Root Locus. The answer should be provided in the format "{w.wwwx.xxx} {y.yyyz.zzz} ..." using three decimal points for all points (rounding or including trailing zeros as needed) from the leftmost to the rightmost interval, so for example "{-Inf -0.987} {-0.500 0.000} {0.560 0.789}". As also seen in this example, if infinity needs to be entered, "-Inf" or "Inf" should be used. If no internal on the Real axis exists in the Root Locus, then "nan" should be entered:

3.Determine the angles, φi, formed with the positive direction of the Real axis by the asymptotes followed by the branches in the Root Locus that terminate at infinity. The answer should be provided in units of degrees in the format "φ1 φ2 φ3 ..." from smaller to larger using no decimal points, so for example "45 135 225 315" If no asymptotes exist in the Root Locus, then "nan" should be entered:

4.Determine the centre of gravity, γ, of the asymptotes of the Root Locus. The answer should be provided in the format "x.xxx" using three decimal points (rounding or including trailing zeros as needed), so for example "-0.123" or "0.123". If no asymptotes exist in the Root Locus, then "nan" should be entered:

5.Determine the departure/arrival points that the branches of the Root Locus depart from or arrive at the Real axis, s0. The answer should be provided in the format "x.xxxy.yyy ..." using three decimal points (rounding or including trailing zeros as needed) from smaller to larger, so for example "-0.123 0.345". If no departure/arrival points exist in the Root Locus, then "nan" should be entered:

6.Determine the angles formed with the positive direction of the Real axis at which the branches emanate from complex poles or poles of multiplicity higher than 1, θ, or arrive at complex zeros or zeros of multiplicity higher than 1, φ, in units of degrees from 0 to 360º. The answer should be provided in the format "θ0 θ1 ... φ0 φ1 ...", using no decimal points so for example "40 320". If all poles and zeros are simple, then "nan" should be entered:

7.Utilise the Routh Hurwitz Stability Criterion to find the ultimate gain, Ku, ultimate frequency, ωu, in units of rad/min, and ultimate period, Tu, in units of min for this system. The answer should be provided in the format "Ku ωu Tu" using three decimal points (rounding or including trailing zeros as needed), so for example "1.123 2.345 6.789". If the system is always stable, then "nan" should be entered:

For all answers above, quotation marks should be excluded when entering data in the answer input text boxes.
Rounding numbers according to above instructions should take place only when these are inputted in the text boxes, not during calculations.
Partial credit is awarded for each fully correct answer in any individual input box, so 35/7 marks are awarded per each of the 7 input boxes containing a fully correct answer.
For internal use only, please disregard: 2211111154

QUESTION 3
For this question consider the system shown in Figure 1. Furthermore, assume the following about its transfer functions:
• Controller: Proportional-Integral with integral time constant equal to 0.24 min.
• Final control element: First order lag with a gain of 1 and a time constant of 0.46 min.
• Process: First order lag with a gain of 1 and a time constant of 0.24 min.
• Measuring device: First order lag with a gain of 1 and a time constant of 0.87 min.
• Disturbance: Same as the process with a gain half of that of the process.
Based on the above data, investigate the frequency response characteristics of this system and give answers for the following:
1.Using the principles of the Bode stability criterion and the correlations that define the amplitude ratio, AR, and the phase shift, φ, determine the values of:

a. The system's crossover frequency, ωco, in units of rad/min. The answer should be provided in the format "x.xxx" using three decimal points (rounding or including trailing zeros as needed), so for example "1.234" or "0.100". If no crossover frequency exists, then "nan" should be entered:

b. The value of the amplitude ratio over the controller's gain, AR/Kc, at the system's crossover frequency. The answer should be provided in the format "x.xxx" using three decimal points (rounding or including trailing zeros as needed), so for example "1.234" or "0.100". If no crossover frequency exists, then "nan" should be entered:

c. The system's ultimate gain, Kcu. The answer should be provided in the format "x.xxx" using three decimal points (rounding or including trailing zeros as needed), so for example "1.234" or "0.100". If no ultimate gain exists, then "nan" should be entered:

2.Tune the controller for the cases below:
a. A gain margin of 1.6. For this, determine the value of the proportional gain of the controller, Kc, that achieves this gain margin. The answer should be provided in the format "x.xxx" using three decimal points (rounding or including trailing zeros as needed), so for example "1.234" or "0.100":

b. A phase margin of 40º. For this case determine the following:
i. The value of the proportional gain of the controller, Kc, that achieves this phase margin. The answer should be provided in the format "x.xxx" using three decimal points (rounding or including trailing zeros as needed), so for example "1.234" or "0.100":

ii. The frequency value at which this phase margin value is observed, in units of rad/min. The answer should be provided in the format "x.xxx" using three decimal points (rounding or including trailing zeros as needed), so for example "1.234" or "0.100":

iii. The value of the amplitude ratio over the controller's gain, AR/Kc, at the frequency determined in part 2.b.ii. The answer should be provided in the format "x.xxx" using three decimal points (rounding or including trailing zeros as needed), so for example "1.234" or "0.100":

For all answers above, quotation marks should be excluded when entering data in the answer input text boxes.
Rounding numbers according to above instructions should take place only when these are inputted in the text boxes, not during calculations.
Partial credit is awarded for each fully correct answer in any individual input box, so 30/7 marks are awarded per each of the 7 input boxes containing a fully correct answer.
For internal use only, please disregard: 1111111138

QUESTION 4
Consider the packed-bed reactor process shown in Figure 2. The inlet stream is pre-heated before entering the reactor in a heat exchanger that operates with hot oil. The control objective is to tightly regulate the exit concentration of the reactor CA(t) via the composition controller AC-1, while the most significant disturbance has been identified to be the heating medium temperature TH(t) measured by sensor TT-1. Due to this, the control engineer has proposed the cascade control scheme shown in Figure 2. The temperature of the reactant stream exiting the heat exchanger TI(t), as measured by sensor TT-2, is used as a secondary control variable. AC-1 generates a temperature setpoint for the secondary controller TC-2 that uses TT-2 readings as its measurement. In turn, this secondary controller regulates the flowrate of the hot oil FH(t).
The relevant transfer functions and the units of their gains are the following, with all time constants appearing below in units of minutes:

Assuming a proportional controller and using the principles of the Routh-Hurwitz stability criterion, determine the ultimate gain Kcu of the secondary control loop.

QUESTION 5
In continuation of the previous question, determine the ultimate frequency of oscillation ωu of the secondary control loop in rad/min.

QUESTION 6
In continuation of the previous question, determine the ultimate period of oscillation Tu of the secondary control loop in minutes.

QUESTION 7
In continuation of the previous question, tune this proportional controller at a gain value equal to half of Kcu.

QUESTION 8
Using the Kc value obtained in the previous question, use the principles of the Routh-Hurwitz stability criterion to find the ultimate gain Kcu of the primary control loop, assuming again a proportional controller.

QUESTION 9
In continuation of the previous question, determine the ultimate frequency of oscillation ωu of the primary control loop in rad/min.

QUESTION 10
In continuation of the previous question, determine the ultimate period of oscillation Tu of the primary control loop in minutes.

QUESTION 11

For the cascade system presented in Figure 2, determine how well it responds to the following disturbances for which it was not specifically designed.

Reactant stream temperature

Reactant stream flowrate

Reactant stream composition

Hot oil pressure
A. Cascade controller is not effective in attenuating this disturbance
B. Cascade controller is partially effective in attenuating this disturbance
C. Cascade controller is effective in attenuating this disturbance

Attachment:- feedback control system.rar