Reference no: EM131478426
Part A
Q1.
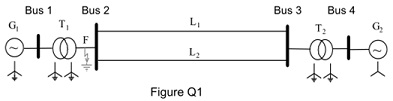
A power network is depicted by Figure Q1. The two generators (G1 and G2 ) are generating at 1 p.u. voltage. The star points of G1 and the two generators T1 and T2 are solidly earthed.
The system reactances are:
G1: X1 = 0.3 , X2 = 0.2 and X0 = 0.05
G2: X1 = 0.25 , X2 = 0.15 and X0 = 0.03
T1: X1 = X2 = X0 = 0.12
T2: X1 = X2 = X0 = 0.1
L1: X1 = X2 = 0.3 and X0 = 0.7
L2: X1 = X2 = 0.3 and X0 = 0.7
All values are in p.u. on the same base.
A double-line to ground fault develops between phases Y and B at Bus 2. Assume the network is initially on no-load:
(a) Determine the symmetrical component networks and calculate the fault current.
(b) A monitoring system is positioned at Bus 4 (between T2 and G2 ). Calculate the three phase voltages at the monitoring point when the fault occurs at Bus 2.
(c) If a reactance is inserted between the neutral point of the alternator G2 and the ground, can the fault current be reduced readily when the fault occurs at Bus 2? Give your explanation.
Q2. (a) With reference to electrical supply, briefly explain what is meant by a ‘power quality' event. State three main effects of harmonic current flow in power systems.
(b) Renewable energy sources are likely to be connected to the distribution power network, hence are called "distributed generation". Comment on the potential benefits (three only) and technical problems (two only) on existing distribution network from large scale connection of distributed generation.
(c) Explain the definition of the distance relay and the operating characteristic of the impedance distance relay.
(d) (i) Give schematic diagrams of one over-current protection and one differential protection schemes which can be used to detect short-circuit faults in the windings of a 3-phase star/delta transformer. For each diagram, show the circuit arrangement including the current transformers and relay coils.
(ii) Comment briefly on the relative merits and disadvantages of the two schemes you give in (i).
Q3. A power plant consists of two multiple-valve generating units with minimum and maximum possible loading for each one of 50 MW and 250 MW. The fuel cost functions (F1 and F2) expressed in £/hour for the two units are given as:
F1 = 0.035P12 + 22P1 + 375 and F2 = 0.045 P22+ 14 P2 + 450
where P1 and P2 are the output powers in MW of the two units, respectively.
(a) Determine and sketch * (on the same graph) the incremental fuel costs (λ1 and λ1 in £/MWh) for each unit over its output power range.
(b) The two units are to run continuously to supply a total plant load that varies between 150 MW and 500 MW.
(i) With reference to the graph in part (a), briefly explain how the two units will have to share the total load in order to minimize fuel costs.
Show that there are three distinct ranges of operation and give the total power supplied at the boundaries of each range.
(ii) For minimum fuel costs, determine the incremental fuel cost of the plant and the load sharing between units (P1 and P2 ) when the plant supplies the following total loads: 150 MW, 300 MW and 475 MW.
Q4. A 3-phase, Y-connected, 6.6 kV, 31.5 MVA turbine generator of 0.85 power factor has a synchronous reactance of 1.2 p.u. on rating.
Neglecting the machine losses, determine:
(a) The real (P) and reactive (Q) power at full load.
(b) The armature e.m.f. (E) and load angle under rated operating conditions.
(c) The maximum Q production assuming the same field current as in part (b)
(d) The Q limit, line current and power factor of the over-excited generator delivering 25.2 MW.
Q5. A 3-phase, 50 Hz, 100 km long transmission line has the following phase parameters per unit length (km): resistance = 0.1 ?, reactance = 0.5 ?, and susceptance = 10 µS. The line supplies an inductive 20 MW load at 66 kV and 0.9 power factor. By applying the nominal π method, calculate:
(a) The sending-end voltage, current and power factor.
(b) The voltage regulation and efficiency of transmission.
(c) The shunt capacitance required at the receiving end of the line to achieve the unity load power factor at 66 kV.
Q6.
A synchronous generator is connected to an infinite bus-bar of 1.0 p.u. voltage as shown by the single line diagram in Fig. Q6. The generator has been producing 1.0 p.u. power with a stator e.m.f. of 1.25 p.u. when a solid 3-phase fault has suddenly occurred on one of the transmission lines near the step-up transformer bus-bar as indicated in the same figure. The fault is cleared by opening the circuit breakers at each end of the affected line which is taken out of commission. All the per-unit (p.u.) quantities are given on a common base.
(a) Derive the power output versus load angle relationships for the pre-fault and post-fault scenarios for the same excitation voltage.
(b) If the peak electrical power of the generator is 0.418 p.u. during the fault interval, sketch the typical power-angle characteristics for the pre-fault, fault and post-fault periods, and then find the critical clearing angle by using the equal area criterion.

Part B
Q1.
(a) Briefly explain the definition of unbalanced faults, and the motivation for the fault level calculation.
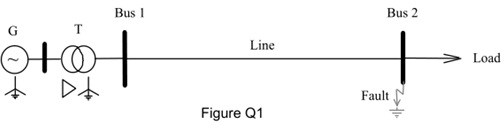
(b) A power network is depicted by Figure Q1. The generator G is generating at 1.2 p.u. voltage. The system component reactances are given as follows:
G: X1 = 0.3 X2 = 0.2 and X0 = 0.05
T: X1 = X2 = X0 = 0.15
Line: X1 = X2 = 0.3 and X0 = 0.5
All values are in p.u. on the same base. Assume the network is initially on no load and a double-line to ground fault develops between phases Y and B at Bus 2.
(i) Determine the symmetrical component networks and calculate the fault current.
(ii) A monitoring system is positioned at Bus 1. Calculate the three phase voltages at the monitoring point when the fault occurs at Bus 2.
According to the monitored voltages at Bus 1, explain how you can identify whether the system is faulty.
Q2.
(a) Define the Smart Grid concept and state three main enabling technologies that will help in realising this concept.
(b) An 11 kV power distribution network is required to supply individual loads which may be arranged into 4 main groups each with an After Diversity Maximum Demand of 800 kW at the lowest possible power factor of 0.8 lagging. The distribution network is to be arranged in open-ring and fed from the grid via two 132/11 kV parallel transformers.
A number of 132 kV / 11 kV transformers of 2 MVA, 3 MVA or 5 MVA rating are available. Stating any assumptions made, select suitable transformers from the above to design a reliable and cost-effective distribution network to supply the above loads. Draw a single-line diagram of your design showing the transformers, cables, isolators and circuit-breakers. Give justification for your design.
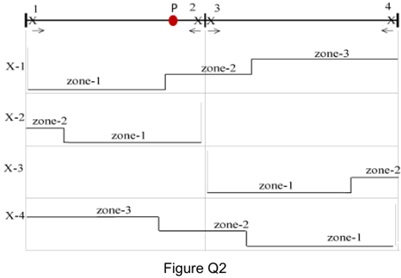
(c) In Figure Q2, there are four distance relays to protect the lines.
(i) Briefly explain the concept and types of the distance relay, and identify the type of the distance relays in Figure Q2.
(ii) What is the 3-zone directional distance protection? When one fault occurs at the P point, explain how the four relays provide the protection.
Q3.
A power generating plant consists of two multiple-valve generating units with maximum possible loading for each one of 300 MW and 500 MW. The plant is connected to the grid network and supplies a total power of 700 MW.
(a) The governor droop characteristics (no-load to full-load percentage speed drop) for the two generating units are 2% and 3%, respectively. The generators operate at 50 Hz at full-load. Assuming a free governor action, sketch the droop characteristics for the two units and calculate the power supplied by each unit and the operating frequency (in Hz) of the plant.
(b) The fuel cost functions (F1 and F2 ) expressed in £/hour for the two generating units are given as:
F1 = 0.045P12 + 12P1 + 375
F2 = 0.04P22 + 12P2 + 450
where P1 and P2 are the output powers in MW of the two units, respectively. Determine the incremental fuel cost (λ) in £/MWh and find the most economical loading of each unit.
What would be the incremental fuel cost for the plant?
(c) Briefly explain how the drop characteristics may be influenced to change the sharing of power between the two units.
Q4.
A 3-phase, 178 MVA, 18 kV, Y-connected synchronous turbo-generator has a synchronous reactance X S = 1.46 ? and a 0.8 power factor lagging under rated operating conditions. A steam turbine driving the generator can deliver a maximum power of 180 MW. The machine is highly efficient so that it can be assumed ideal for convenience of analysis.
(a) By means of the approximate equivalent circuit or the corresponding phasor diagram, show that the generator rotor limit in terms of the 3- phase powers and line-to-line voltages using standard notation can be expressed as:
P2 + (Q + V2/Xs)2 = (V.Emax/Xs)2 = P2max
Explain the meaning of the generator static stability limit (Pmax ) formulated above.
(b) Sketch the capability curve of the generator in a (P, Q) plane clearly indicating the portions of the specific circular operating limits it is made of, and providing the relevant details on the respective centres/radii as well as the associated cross-over points.
(c) Determine the maximum reactive power (Q) the machine can exchange with the grid when (1) over-excited and (2) under-excited. What is the reference (positive) Q flow in each case?
(d) Calculate the rms values of the induced voltage and stator current for the machine ‘natural' excitation mode in part (c).
Q5.
A 3-phase short transmission line supplies a Y-connected inductive industrial load of 500 kW at V R = 3.3 kV (rms) and 0.8 power factor. The line resistance is R = 2.5 ? and a reactance is X = 4.33 ? per phase.
(a) Calculate the voltage regulation and transmission efficiency of the line.
(b) If a 3-phase, Y-connected synchronous motor was used as a synchronous condenser, what motor current would be required to achieve the unity power factor at the receiving (load) end? Comment on the implications of such or similar Q compensation method on efficiency of transmission.
(c) Using a simplified algebraic expression for the voltage drop across the line:
ΔV = VS - VR ≈ (RP + XQ)/VR ....
where P,Q are the real and reactive power demands of the load, find the sending-end (V S ) voltage before and after Q compensation. From the results obtained, draw suitable conclusions about the Q compensation effects on V.
Q6.
A turbo-generator delivers rated power to an infinite bus-bar through a mostly reactive network of negligible resistance. A balanced fault occurs in the system resulting in the temporary loss of the entire generated power. Before the fault inception the maximum power transferable to the load was 1.8 p.u., and after the fault clearance it dropped to 1.3 p.u. The generator losses can be ignored.
(a) Sketch the power curves for the pre-fault, fault and post-fault periods, and calculate the steady-state load angles of the generator before and after the fault.
(b) Making use of the equal-area criterion, estimate the critical clearing angle.
Why is this angle, and the corresponding critical clearing time, important for transient stability of a power system?