Determine the rejection region and state your conclusion

Assignment Help Applied Statistics

Reference no: EM131745496

Homework-

Assume we are interested in fitting an additive multiple regression model of Y on four potential covariates X₁, X₂, X₃, X₄ : , i.e. our model is Y_i = β₀ + β₁X_i1 + β₂X_i2 + β₃X_i3 + β₄X_i4 + ε_i, i = 1,...,n , where εi ~^i.i.d.N (0, σ²) . The sample size is n = 17 and SST0 = 1062.21.

a) Define C′ and m for the composite hypothesis that β₀ = 0, β₁ + β₂ = 0, and β₃ = β₄. That is, express as

H₀: C'β = m

H_a: C'β ≠ m

b) Give the rank of C′.

c) State the reduced model for the composite hypothesis in part (a).

d) The SSE for the model Y_i = β₀ + β₁X_i1 + β₂X_i2 + β₃X_i3 + β₄X_i4 + ε_iis 37.88 and the SSE for the reduced model in part (c) is 95.11. Use the general linear test to test the hypothesis in part (a). Compute the value of the test statistic, determine the rejection region, and state your conclusion.

Note: The test statistic should be expressed in fraction form: #/# ÷ #/# as well as computing the value.

e) Compute R² and R²_adj for the model Y_i = β₀ + β₁X_i1 + β₂X_i2 + β₃X_i3 + β₄X_i4 + ε_i.

A summary of influence measures for the model Y_i = β₀ + β₁X_i1 + β₂X_i2 + β₃X_i3 + β₄X_i4 + ε_iis given below:

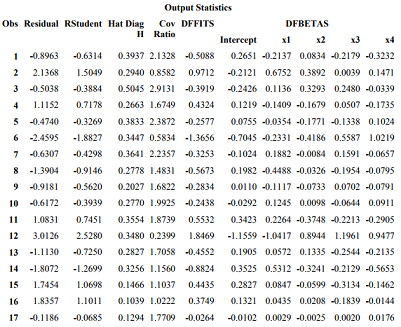
f) Identify which observation(s) is/are outliers, if any. Use a cutoff of 2.

g) Identify which observation(s) is/are high leverage points, if any.

h) Identify which observation(s) is/are influential on the fitted values, Y^ˆ_i , if any.

i) Identify which observation(s) is/are influential on the estimate of β₀, if any.

j) Identify which observation(s) is/are influential on the estimate of β₁, if any.

k) Identify which observation(s) is/are influential on the estimate of β₂, if any.

l) Identify which observation(s) is/are influential on the estimate of β₃, if any.

m) Identify which observation(s) is/are influential on the estimate of β₄, if any.

Attachment:- Assignment.rar

Reference no: EM131745496

Questions Cloud

How much time should co teachers spend together to plan : How much time should co teachers spend together to plan? What happens when you can't find a mutual time for planning?

How does social anxiety and social loafing relate to virtual : How does social anxiety and social loafing relate to virtual groups. Do virtual groups make these problems more difficult or less difficult to address

Find the equation of the least-squares regression line : Popularity of a first name. The Social Security Administration maintains lists of the top 1000 names for boys and girls born each year since 1879.30

Are opportunities for development growing or diminishing : Are opportunities for development growing or diminishing? Does the Internet provide opportunities for development with limited trade-offs?

Determine the rejection region and state your conclusion : STA 403/503 Homework. Use the general linear test to test the hypothesis in part (a). Compute the value of the test statistic, determine the rejection region

How do we know which operators to use in java : How often do we use primitive variables when we are creating a code in a program? Do we use them all the time or very seldom?

Discuss what are the elements of romanticism : what are the elements of romanticism in this passage and how does it develop the plot

Does the case appear to work for or against your client : Fozze Bear, stands convicted for the heinous murder of Miss Piggy. Does the case appear to work for or against your client?

What role does art making or art viewing have in your life : What was the very first artwork you remember doing? How did you feel about it when you made it? What role does art making or art viewing have in your life?

User Account

All Pages