Reference no: EM13214136

Question 1

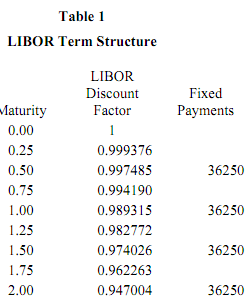
We want to value a 2 year interest rate swap, assuming the floating side is reset every three months, while the fixed rate payments are every six months. The fixed rate payments are given in Table 1. The notional value of the swap is $1 mm. Given the information in the Table,

please answer the following questions.

(a) Determine the present value of the floating rate payments.

(b) Determine the present value of the fixed rate payments?

(c) Determine the value of the swap to the party receiving floating, paying fixed.

Question 2

Suppose now that the floating side is reset to LIBOR + 20 basis points. Given the information in Table 1 and Question1, please determine

(a) the present value of the floating rate payments;

(b) the present value of the spread component; remember the floating payments are made every quarter.

(c) Determine the value of the swap to the party receiving floating paying fixed.

Question 3

Consider an asset swap. The Bank makes a loan to a borrower, full value $94.38 (quoted on a per 100 face value). The face value of the loan is $1 mm. and the coupon of $36,250 per $1 mm. face value every six months. We have lent 1mm to the borrower and the present value of the payments from the borrower is $94.38 per 100 face value.

Consider first the net present value of the interest rate swap to the bank. Remember the bank receives the floating payments and makes fixed payments of $36,250 to the swap institution.

We want to determine the net present value of the swap to the bank. We have shown that this can be written as 100 + S * Annuity - Bond(C), assuming face value of 100.

(a) Determine the present value of the bond payments; that is B(C). Remember the coupon is paid every six months.

(b) Determine the present value of the annuity. Remember the annuity is paid every quarter.

(c) Determine the minimum spread, using the information in Table 1.

(d) What other risks is the bank exposed to in making an asset swap?