Reference no: EM132807987

QUESTION

(1) Let f (x) = -196x₁ - 103x₂ + 1/2(37x₁1² + 13x₂² + 32x₁x₂).

(a) Use the eigenvalues and eigenvalues of the Hessian matrix to sketch the level sets of f (x).

(b) Give a graphical solution to the problem of minimizing f (x) subject to the constraints:
- x₁ + x₂ ≤ 0,

x₁ ≤ 3,

-x₂ ≤ 0.

(c) Show graphically that the optimality conditions are satisfied.

(2) A QP computer code is used to solve min{ f (x) = c'x + 1/2x'Cx|Ax ≤ } where

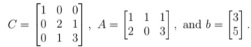
You pick three choices of c, namely,

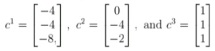
and in all cases, the compute code gives the wine global minimizer x* = [1 1 1]'. Can this code be trusted?

(3) The problem min{ -μ'x | x ≥ 0, l'x = 1 is to maximize returns subject to no short, sales.

Determine the optimal solution and verify your solution by showing that the optimality conditions are satisfied.

(4) Is x* = (1, 2, 3)^T the optimal solution to the following QP?

Minimize Q(x) subject to = x₁ -2x₂ -x₃ + 1/2x₁² -x₁x₂ + x₂² - 2x₂x₃ + 2x₃²

x₁ + x₂ ≤ 10,

2x₁ + 3x₃ ≤ 11,

-2x1 + 2x2 -5x3 ≤ -13

-x₁ ≤ 0,

-x₂ ≤ 0,

-x₃ ≤ 0,

(5) The linear complementarity problem is to find vectors w and z that satisfy w =Mz + q, w ≥ 0, z ≥ 0, and w'z = O. where M is a given (square) matrix and q is a given vector. Show that if

m  [C -A']                                [c] 
    [A   0 ]                    and q = [-b]

then a solution to the complementarity problem is a solution to the quadratic programming problem min{ f (x) = c'x + (1/2)x'Cx|Ax ≥ b, x ≥ 0}.