Reference no: EM132323802

Further Mathematics for Construction Assignment -

In this assessment you will have opportunities to provide evidence against the following criteria. Indicate the page numbers where the evidence can be found.

P1 - Apply addition and multiplication methods to numbers that are expressed in different base systems.

P2 - Solve construction problems using complex number theory.

P3 - Perform arithmetic operations using the polar and exponential form of complex numbers.

P4 - Ascertain the determinant of a 3x3 matrix.

P5 - Solve a system of three linear equations using Gaussian elimination.

P6 - Estimate solutions of sketched functions using graphical estimation method.

P7 - Identify the roots of an equation using two different iterative techniques.

P8 - Determine the numerical integral of construction functions using two different methods.

P9 - Determine first-order differential equations using analytical methods.

P10 - Determine second-order homogenous and non-homogenous differential equations using analytical methods.

P11 - Calculate solutions to linear ordinary differential equations using Laplace transforms.

M1 - Deduce solutions of problems using de Moivre's Theorem.

M2 - Determine solutions to a set of linear equations using the inverse matrix method.

M3 - Solve construction problems and formulate mathematical models using first-order differential equations.

M4 - Evaluate how different models of construction systems use first-order differential equations to solve structural or environmental problems.

D1 - Test the correctness of a trigonometric identity using de Molvre's Theorem.

D2 - Validate all analytical matrix solutions using appropriate computer software.

D3 - Critique the use of numerical estimation methods, commenting on their applicability and the accuracy of the methods.

D4 - Evaluate first- and second-order differential equations when generating the solutions to construction situations.

Learning Outcomes -

1. Apply instance of number theory in practical construction situations.

2. Solve systems of linear equations relevant to construction applications using matrix methods.

3. Approximate solutions of contextualised examples with graphical and numerical methods.

4. Review models of construction systems using ordinary differential equations.

1. a. Sum the following numbers expressed in their respective bases:

• 11001100112
• 52014378
• 93D462C16

Convert each number into denary, along with the answer to verify your result.

2. The characteristic impedance (Z0) and the propagation constant (C) of a transmission line are given by:

Z0 = ZY and C = ZY

Where:

• Z is the series impedance in Ω.
• Y is the admittance of the line in Ω.
• Re (Z0) >0 and Re (C) >0.

Find Z0 and C when: Z0 = 0.11+0.41j and Y= (1-250j)x10-8

3. a. A system has an open-loop transfer function (G) given by: G = 100/(10e^j(π/2)1.02e^j0.21.8e^j0.99)

Simplify G.

b. Express the following voltage in complex exponential form: v=20sin (1000t-30^o) volts.

Find a formula for cos (3θ) in terms of cos (θ) and sin (θ) using de Moivre's Theorem. (M1)

Prove cos2θ =cos²θ -sin²θ and sin2θ = 2sinθcosθ, using de Moivre's Theorm (D1)

4. Evaluate the value of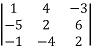

5. Solve the following system of equations using Gaussian elimination.

-3x + 2y - 6z = 6

5x + 7y - 5z = 6

x + 4y - 2z = 8

Use matrices to solve the simultaneous equations: (M2)

x + y + z = 4

2x - 3y + 4z = 33

3x - 2y - 2z = 2

Validate matrix solutions calculated in Task M2 using Microsoft Excel (e.g. the programming step is expected to be stated). (D2)

6. Solve the quadratic equation 4x² + 4x -15=0 graphically given that the solutions lie in the range x = -3 to x = 2.

7. Use Newton's method to determine the positive root of the quadratic equation 5x² + 11x - 17 = 0, correct to 3 significant figures. Check the value of the root by using the quadratic formula.

8. Evaluate ₁∫³2/√x dx,

a) Using the trapezoidal rule with 4 intervals, correct to 3 decimal places.

b) Using the mid-ordinate rule with 4 intervals, correct to 3 decimal places.

The bending moment M of the beam is given by dM/dx = -w(l-x) where w and x are constants. Determine M in terms of x given: by M = ½ wl² when x = 0. (M3)

Followed by P8, evaluate ₁∫³2/√x dx, using the Simpson's rule with4 intervals, correct to 3 decimal places. Based on the result of using three different methods, comment their applicability and accuracy. (D3)

9. The current i in an electric circuit containing resistance R and inductance L in series with a constant voltage source E is given by the differential equation E - L (di/dt) = Ri. Solve the equation and find i in terms of time t given that when t = 0, I = 0.

10.

L d²q/dt² + R dq/dt + 1/c q = V_o sinωt

represents the variation of capacitor charge in an electric circuit.

Given that R = 40 Ω, L = 0.02H, C = 50 x 10-6 F, Vo = 540.8V and ω = 200 rad/s and also given the boundary conditions that when t = 0, q =0 and dq/qt = 4.8.

Solve problem using initial and boundary value conditions to determine an expression for q at t second.

11. Solve using the Laplace transform

y' - y = e^3t, y(0) = 2

In an alternating current circuit containing resistance R and inductance L the current i is given by: (M4)

R_i + L di/dt = E₀sinωt

Given i = 0 when t = 0, select appropriate differential equation model to show that the solution of the equation is given by: (hint: partial differential model to set up second order differential equation or others)

i = (E₀/(R²+ ω²L²)) (Rsinωt - ωLcosωt) + (E₀ωL/(R²+ω²L²))e^-Rt/L

(a) The variation of resistance R ohms, of an aluminum conductor with temperature θ^oC is given by dR/dθ = αR, where α is the temperature coefficient of resistance of aluminum. If R = R₀ when θ = 0^oC, solve the equation for R.

(b) If α = 38x10^-4/^oC, determine the resistance of an aluminum conductor at 50^oC, correct to 3 significant figures, when its resistance at 0^oC is 24.0 Ω. (D4)

Submission Format: The submission is in the form of essay writing and presentation format, it is required to follow the instructions from each task. The essay should be written in a concise and formal business style. As such, your choice of font and font size should contribute to the clarity of the information. The essay should be well-structured, using tasks, using headings, sub-sections and paragraphs as appropriate. Any images, graphics, or text that is derived from other sources must be correctly referenced using a standard form of citation. A bibliography should be included and in a standard academic format. The recommended word is around 5,000 words and at least 3 pages of answers to each question.