Reference no: EM131083662
Math 171: Abstract Algebra, Fall 2014- Assignment 6
1. In each of the following, given a group G, a set X and an operation · : G × X → X, determine if · is a group action:
(a) G = D8, X = G, and for any g ∈ G, x ∈ X,
g · x = xg
(b) G is any group, X = G, for any g ∈ G, x ∈ X,
g · x = gxg-1
2. Let G be a finite group acting on a finite set X.
(a) Define the relation ∼ on X by x ∼ y if x ∈ Gy. Prove ∼ is an equivalence relation.
(b) The equivalence classes of X under ∼ are called the distinct orbits of the action of G on X. Why is that name appropriate?
(c) Let X be the set of colorings of a 2 × 2 grid where each grid is colored red or green. Let G be the subgroup of D8 given by G = {1, r, r2, r3}. Then G acts on X; rk rotates the grid clockwise 90k degrees. Determine the distinct orbits of the action of G on X.
3. A group G is solvable if there is a chain of subgroups
1 = G0  G1
G1  G2
G2  · · ·
· · ·  Gs = G
Gs = G
such that Gi+1/Gi is abelian for i = 0, 1, . . . ,s - 1.
(a) Determine, with justification, if S4 is solvable.
(b) Let G be a group with a normal subgroup N  G such that N and G/N are solvable. Prove
G such that N and G/N are solvable. Prove
G is solvable.
(c) Mathematicians consider the problem of determining if a group is solvable or not to be analogous to prime factorization. Give a brief explanation of why this would make sense?
4. (a) Let M, N be normal subgroups of G such that G = MN. Prove G/(M ∩ N) ≅ (G/M) × (G/N).
(b) Conclude the Chinese Remainder Theorem: If m, n ≥ 2 are integers and gcd(m, n) = 1 then Z/mnZ ≅ Z/mZ × Z/nZ.
(These are additive groups, so remember MN is the set of sums of elements from M and N.)
(c) How does part b) prove the Chinese Remainder Theorem from Math 55? Namely that if gcd(m, n) = 1 with m, n ≥ 2, and a, b ∈ Z, then there is a unique solution mod mn to the system of congruence equations
x ≡ a ( mod m), x ≡ b ( mod n).
5. Read the following article "IDcheckdigit.pdf" on the class webpage. The link is right under the link for Assignment 6. Answer the following related questions:
(a) Provide an example not given in the paper that illuminates the key difference(s) between two Identification Number schemes of your choice.
(b) Write a one page exposition that illuminates the power that group theory has in providing check digits for Identification Numbers. In particular, discuss how this power is reflected in Verhoeff's idea over other Identification Number practices.
Article - The Mathematics of Identification Numbers
Stable URL:
https://links.jstor.org/sici?sici=0746-8342%28199105%2922%3A3%3C194%3ATMOIN%3E2.0.CO%3B2-Q
6. Watch this video:
https://www.youtube.com/watch?v=8M4dUj7vZJc
(Please ignore their attempt at humor. Moreover, observe they multiply transpositions in the wrong way at around time 2:40!) Explain how the problem presented in the video relates to its mathematical re-statement and proof as presented in the video. Describe the proof in a way that someone who doesn't have a group theory background could understand it.
7. (a) Is the following statement true: If G is a group and H is a normal subgroup, then the order of Hy in G/H divides the order of y in G.
(b) Prove A4 has no subgroup of order 6. (Hint: First prove any element of such a subgroup must have odd order.)
8. A coloring of the grid below is an assignment of colors to its triangular cells, where any given triangular cell is colored red or green. Determine the number of colorings of the grid, with the condition that two colorings are considered the same if one can be obtained from the other by rotating the grid about its center.
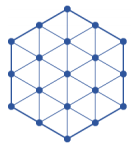
What if we now also allow reflectional symmetry?