Reference no: EM132012698

Vibration Analysis Questions -

Q1. Determine the normal modes and frequencies of the system shown in Fig.

Q2. Determine the normal modes of the torsional system shown in Fig. for K₁ = K₂ and J₁ = 2J₂.

Q3. Determine the natural frequency of the torsional system shown in Fig. and draw the normal mode curve. G = 80GPa.

Q4. An electric train made up of two cars of weight 22680 kg each is connected by couplings of stiffness equal to 2803 kN/m as shown in Fig. Determine the natural frequency of the system.

Q5. Assuming small amplitudes, set up the differential equation of motion for the double pendulum using the coordinates shown in fig. Show that the natural frequencies of the system are given by the equation ω=√(g/l (2±√2)).

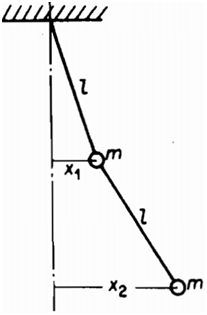
Determine the ratio of amplitudes x₁/x₂ and locate the nodes for the two modes of vibration.

Q6. Two masses m₁ and m₂ are attached to a light string with tension T, shown in Fig. Assuming that the tension T remains unchanged when the masses are displaced normal to the string, write the equations of motion expressed in matrix form.

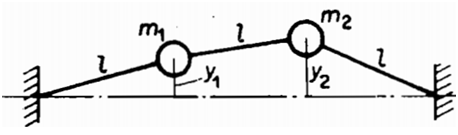
Q7. Choose coordinates x for the displacement c and θ clockwise for the rotation of the uniform bar shown in Fig., and determine the natural frequencies and mode shapes.

Q8. For the system shown in Fig., W₁ = 90 kg and the absorber weight W₂ = 23 kg. If W1 is excited by a 0.023 kg-m unbalance rotating at 1800 rpm, determine the proper value of the absorber spring k₂.What will be the amplitude of W₂.