Reference no: EM132789465

Portfolio Optimization

(1) Show that l'h₁ = 0.
(2) Is h₀ ≥ 0? Prove or give a counter example.
(3) Show that h₁ = 0 if µ is a multiple of l.
(4) Show that β₁ = 0.
(5) Show that β₂ = α₁.
(6) Explain why, if µ = rl, we get σ²_p = 0.

(7) Consider the inequality

r < µ' [Σ^-1 l/l'Σ^-1l]

(a) Derive the inequality.
(b) Explain its importance.
(c) Interpret the right-hand side as an expected value.

(8) We have two investors, named X and Y, with perfect market information. Each has invested a total of $100,000. Their aversion to risk is determined by their t values of tx and ty, respectively. Investor X's portfolio in the risky assets is given by

(a) How much has Investor X invested in the risk-free asset?

(b) Suppose that 20% of Investor Y's portfolio is invested in the first risky asset. How much has Investor Y invested in the risk-free asset?

(9) Please summarize your answers to the given questions on paper separate from your rough work. Your rough work can be on paper or on a spreadsheet (that I can understand) that is e-mailed to me. Let

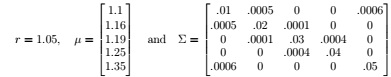
(a) Determine the parametric efficient portfolio x(t).

(b) Determine the expected value and the variance for x(t), that is, determine µp(t) and σ_p²(t).
(c) Determine the constants c1, c2, and c3 so that the efficient frontier is given by

σ² = c₁µ_p² + c₂µ_p + c₃.

(d) What is (σˆ2, µˆ), the point on the efficient frontier corresponding to the minimum variance portfolio, on the variance-expected value coordinate system?

(e) What is (σˆ, µˆ), the point on the efficient frontier corresponding to the minimum vari-ance portfolio, on the standard deviation-expected value coordinate system?

(f) Determine the market portfolio x_m and the corresponding values of σ_m and µ_m.

(g) Determine c₄ and c₅ so that the Capital Market Line is given by the equation

µ_p = c₄ + c₅σ_p.

Show that (σ_m, µ_m) is a point on the Capital Market Line.

(h) Find c₆ and c₇ so that the Security Market Line (SML) is given by

µ_i = c₆ + c₇ (cov(ri, rm)).

Show that, for i = 1, 2, 3, 4, 5, the point (Σ_ix_m, µ_i), where Σ_i is the i-th row of Σ, is on the SML. Show that xm is on the SML, that is, show that (σ2 , µm) satisfies your equation for the SML.

(i) Suppose that µm = 1.2. Determine the corresponding tm and σ_m. Determine an equation for the implied CML and determine the implied risk free return.

Attachment:- Portfolio Optimization.rar