Reference no: EM132331590

Question 1

The MATLAB file psa9p12.m or psay11_a2q1.m or other power flow software should be used for this question.

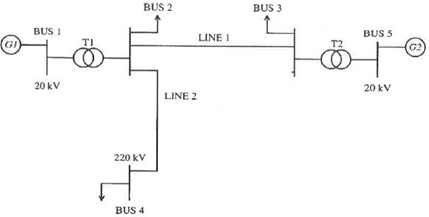
LOADS (at peak time)

BUS 2: 60 MW + 12 MVAr

BUS 3: 60 MW + 12 MVAr

BUS 4: 120 MW + 0 MVAr

Generation

Active power from G2 = 120 MW (at peak time); Bus 1 is the swing bus

Bus voltages

Voltages at bus 1 and bus 5 fixed at 1 pu by the AVRs (automatic voltage regulator) of the generators.

Bus 2, Bus 3 and Bus 4 are load buses (or PQ buses or bus type 1).

Transformers Ratings

Transformer rating (both) : 180 MVA Tap position fixed at nominal value Line Ratings:
All lines: 480 A

Generator Ratings:

For each generator, Active Power Limit = 150 MW; MVA limit = 180 MVA

System data (common MVA base of 200)

Series impedance for T1 = 0.02+ j0.12 pu Series impedance for T2 = 0.02+ j0.10 pu
Per phase series impedance for line 1 = (0.05 + j 0.125) pu = 12.1+ j 30.3 Ω Per phase series impedance for line 2 = (0.1 + j 0.25) pu = 24.2 + j 60.6 Ω Per phase susceptance for line 1 = 0.0303 pu = 125 μS
Per phase susceptance for line 2 = 0.0605 pu = 250 μS

(a) Determine the bus voltages in pu at system peak. Do you detect any problems?

(b) Determine the required level of VAR generation at bus 4 if voltage at that bus is to be brought up to 1 pu at system peak load. (Assume there is a synchronous condenser available at bus 4).

(c) The geographical distance between bus 2 and bus 4 is the same as the distance between bus 3 and bus 4. A new transmission line (line 3) will be installed between bus 3 and bus 4. It will have the same electrical characteristics as line 2. State one major operational benefit that will result from line 3. Justify and illustrate by appropriate quantitative analysis.

Question 2

Use a common base MVA of 100.

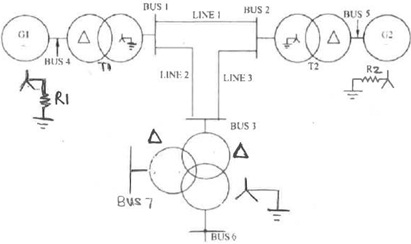
Table 1: System impedance

Plant	Rated voltage kV	Rated MVA	X+ pu	X- pu	X° pu
G1 R1= 0.5 Ω	20	200	0.25	0.15	0.08
G2 R2=0.5 Ω	25	300	0.2	0.15	0.1
T1	20/220	350	0.10	0.10	0.10
T2	25/220	350	0.10	0.10	0.10
T3	220/66/11	200	0.04 per winding	0.04 per winding	0.04 per winding
L1 80 km	220	n/a	j 0.5 Ω/km	j 0.5 Ω/km	j 1.1 Ω/km
L2 100 km	220	n/a	j 0.5 Ω/km	j 0.5 Ω/km	j 1.1 Ω/km
L3 120 km	220	n/a	j 0.5 Ω/km	j 0.5 Ω/km	j 1.1 Ω/km

Assumed prefault conditions: system unloaded with all bus voltage = 1 pu

(a) Draw the positive, negative, and zero sequence networks for the system. Include all impedance values.

(b) A three phase bolted fault occurs on line 2 at a point equidistant between bus 1 and bus 3.

Calculate the following currents (in amperes): The Fault current
Line current for Generator 1 Line current for Generator 2

(c) Assume that a single line to ground bolted fault occurs at bus 3. Using the networks from (a), calculate (in ampere) the resulting fault current.

Question 3

Repeat example 13.9 of your textbook with the same loading limits and coefficients as given in table 13.5 and start-up cost of $3000 and shut-down cost of $1500 respectively. However the loading given in figure 13.11 is now changed to:

Stage Number	1 (0-4 am)	2 (4-8am)	3 (8-12 pm)	4 (12-4pm)	5 (4-8pm)	6 (8-12am)
Load (MW)	900	1200	1400	1600	1200	900

Question 4

Repeat question 3 above for the case of a competitive electrical energy market set to supply electricity for a community on a relatively small island with an electricity network not connected to any external networks. Transmission losses may be neglected. Each one of the four generators is owned by a separate private company which is a market participant. The competitive electricity market consists of (a) a capacity market (b) a day ahead market and (c) a frequency control market. The capacity market may be considered settled and is not relevant to this question. Generators may simultaneously participate in both the frequency control market and the day ahead market. However if a generator is providing frequency control services then its set point should be no lower 25 MW above its minimum loading limit and no higher than 25 MW below its maximum loading limit. This is to allow control of frequency under normal fluctuations of load. Generators providing frequency control services are paid a fixed amount of $5000 for every dispatch period of 4 hours. You may assume that any participant is paid the fixed amount of $5000 if their generator is on- line during any one of the 4-hour dispatch period. However here the principle is being applied to a four hour dispatch period.

For simplicity, assume that each participant's bid is the same for all of the six dispatch interval shown above.

(a) If you were the owner of generator unit number one, what as participant in the day ahead market would be your bid? Explain the basis of your bid.

(b) Assuming reasonable bids from the other three participants, determine the market clearing price for the six dispatch intervals.

(c) Calculate total revenue and profits for each participant for the 24-hour period.

Note: Want the solution of all problems except Question 2.