Reference no: EM131609

Problem 1. Solve the following functions for x (where x is a real number). Leave your answers in exact form, that is, do not use a calculator, show all working.

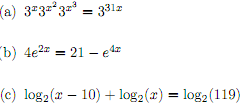
Problem 2. A manager has determined the cost C, in dollars, for manufacturing is

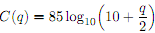
for manufacturing, where q is the number of units produced in a given day.

(a) What is the cost of manufacturing before any units are produced?

(b) What is the cost of manufacturing if 1980 units are produced in a given day?

(c) How many units would be produced if the cost of manufacturing is $150 in a given day?

Problem 3. Find all solutions of the following equations in the interval [0, 2π)

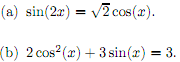
Problem 4. (a) Sketch the graph of the circular function

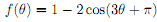
i. State clearly the amplitude, phase shift, period and the equation of the midline.
ii. Show working for all θ- and y-intercepts for the function y = f(θ).
iii. Show at least two periods for the graph of y = f(θ), and label the axes clearly.

(b) Prove the following identity

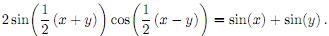
Make sure you show all working and give clear explanations.

Problem 5. Consider the function

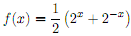
which has the graph

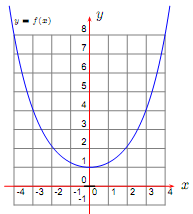
(a) Explain why f has no inverse function. You should include an example to support your explanation.

(b) Determine the largest possible domain, which includes x = 1, for f(x) such that the inverse function f^-1(x) does exist.

(c) Given your answers in (b) ?nd the inverse function f^-1(x). Clearly explain key steps and show all working.

(d) Sketch the graph of y = f(x) for the restricted domain in (b) and y = f-1(x) on the same set of axes. All points of intersection and axes-intercepts should be easily determined from your sketch or clearly labelled. Furthermore axes should be clearly labelled with appropriate scaling.