Reference no: EM13249803

1. Sketch the following function

f(t) = 4 0 < t < 2

f(t) = t²  t ≥ 2

Determine the Laplace transform of the function by writing the function in terms of Heaviside functions.

2. Use the method of Laplace transforms to solve the initial value problem

y' + 2y = 4t

subject to the initial condition y(0) = 5.

3. Determine the Laplace transforms of the following.

tsinh(8t)

te^tH(t-4)

4. Determine the inverse Laplace transforms of the following transform. using the method as indicated.

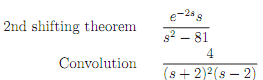
5. Evaluate the following integral

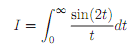
using the general result for Laplace transforms of the type f(t)/t.

6. Solve the initial value problem

y'' + 2y' + 2y = e^-t

subject to the initial condition y(0) = 0 and y'(0) = 1.

7. Solve the initial value problem

y'' - 2y = δ(t-1)

subject to the initial condition y(0) = 1 and y'(0) = 0.

Sketch the solution in the interval t ∈ [0, 2].

8. Use the method of Laplace transforms to determine the subsidiary equation for subject to the initial conditions

y''' + y'' - y' - y = 0

subject to the initial conditions

y(0) = 1

y'(0) = -1

y''(0) = 1

You do not have to determine y(t), you only have to determine the subsidiary equation.

9. You are required to determine the decay curves for radioactive decay of a set of heavy isotopes. The isotope, ²³⁴U decays into ²³⁰Th with a half-life of 246000 years. The isotope, ²³⁰Th decays into ²²⁶Rn with a half-life of 75380 years. The isotope, ²²⁶Rn decays with a half-life of 1600 years.

You should construct a set of coupled linear differential equations that describes the time evolution of the system.

Then use Laplace transformations to determine the functions that describe the time evolution of ²³⁴U, ²³⁰Th, and ²²⁶Rn. for some radioactive material that initially contains 2.0 mols of ²³⁴U and 0.010 mols of ²³⁰Th.