Reference no: EM131444069

Problem 1

A position-time graph for a particle moving along the x-axis is shown in figure to the right.

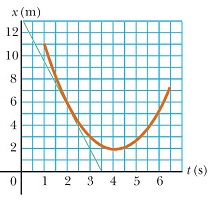
a) Find the average velocity in the time interval t = 1.50 s to t = 4.00 s.

b) Determine the instantaneous velocity at t = 2.00 s by measuring the slope of the tangent line shown in the graph.

c) At what value of t is the velocity zero?

Problem 2

What is the instantaneous velocity of a freely falling object 10 s after it is released from a position of rest? What is its average velocity during this 10-s interval? How far will it fall during this time?

Problem 3

A ball is tossed with enough speed straight up so that it is in the air several seconds.

a) What is the velocity of the ball when it reaches its highest point?

b) What is its velocity 1 s before it reaches its highest point?

c) What is the change in its velocity during this 1-s interval?

d) What is its velocity 1 s after it reaches its highest point?

e) What is the change in velocity during this 1-s interval?

f) What is the change in velocity during the 2-s interval? (Careful!)

g) What is the acceleration of the ball during any of these time intervals and at the moment the ball has zero velocity?

Problem 4

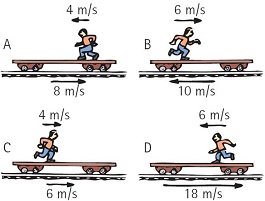
Jogging Jake runs along a train flatcar that moves at the velocities shown in positions A-D. From greatest to least, rank Jake's velocities relative to a stationary observer on the ground. (Call the direction to the right positive.)

Problem 5

Here we see top views of three motorboats crossing a river. All have the same speed relative to the water, and all experience the same river flow. Construct resultant vectors showing the speed and direction of each boat. Rank the boats from most to least for

a) the time to reach the opposite shore.
b) the fastest ride.
c) the shortest path.

Problem 6

On which of the below hills does the ball roll down with increasing speed and decreasing acceleration?

Problem 7

As seen from above, a stubborn stump is pulled by a pair of ropes, each with a force of 200 N but at different angles, as shown. From greatest to least, rank the net forces on the stumps. Give a pictorial representation to support your answers.

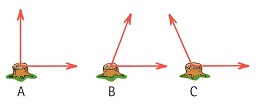
Problem 8

Nellie hangs motionless by one hand from a clothesline. Which side of the line, (a) or (b), has the greater tension? Draw a diagram supporting your answer.

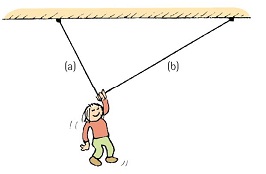
Problem 9

A jet plane comes in for a landing with a speed of 100 m/s, and its acceleration can have a maximum magnitude of 5.00 m/s2 as it comes to rest.

a) From the instant the plane touches the runway, what is the minimum time interval needed before it can come to rest?
b) Can this plane land on a small tropical island airport where the runway is 0.800 km long? Explain your answer.

Problem 10

A ball is thrown directly downward, with an initial speed of 8.00 m/s, from a height of 30.0 m. After what time interval does the ball strike the ground?

Problem 11

During a track event two runners, Bill and John, round the last turn and head into the final stretch with Bill a distance d in front of John. They are both running with the same velocity rO. When the finish line is a distance s away from John, John accelerates at a constant aJ until he catches up to Bill and passes him. John then continues at a constant speed until he reaches the finish line.
a) How long did it take Jim to catch Bob?
b) How far did Jim still have to run when he just caught up to Bob?

Problem 12

When an object is in mechanical equilibrium, what must be stated about all the forces acting on the object?