Reference no: EM13122649
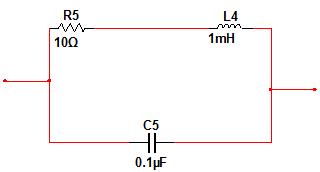
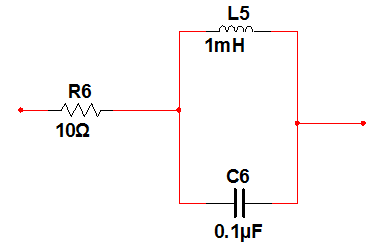
Redraw the following schematics with the impedance of each of the element shown in Laplace domain. Then determine the overall impedance of the entire circuit between the two ends of the shown circuit and express it in Laplace domain as a ratio of two polynomials in s, with the coefficients of the highest power if s in the numerator and denominator are made unity. (Follow the method outlined in the lecture to determine the impedances of elements in Laplace domain and then use the formulas for combining impedances in series and parallel.)
(a) Apply Laplace transform to the following differential equation and express it as an algebraic equation ins.
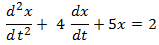
(b) Given that all initial conditions are zero,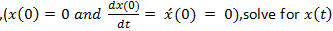 
,solve for x(t) as a function of time by inverting x(s) using Laplace transform pair tables. Show the steps you took in finding the answer.
Hint: Make use of the following Laplace transform pairs in this and following problems.
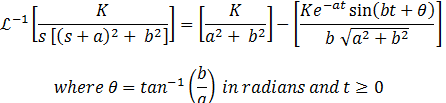
The above formula is used when the roots of the algebraic equation obtained by applying Laplace transform to the differential equation are complex. When roots are real, we use the following:
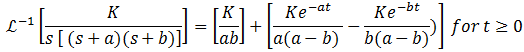
(c) Now solve the differential equation using the "Dsolve"command of MATLAB as explained in the lecture for Week 2.Paste your MATLAB commands and answers obtained below and prove that the two answers (one obtained by inverting using Laplace tables in part (b) and the answer provided by MATLAB) agree by solving for value of x(t)att= infinity and t = 0 seconds in both cases. This shows that the same expression can be represented in more than one form. Trigonometric identities can be used to show that the two expressions are the same, though you are not required to do that as part of the homework.
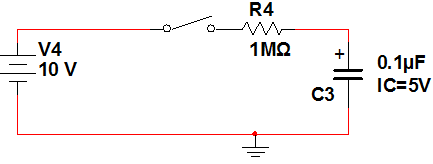
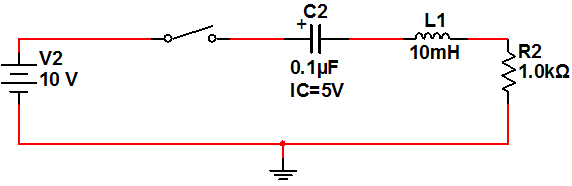
An RC circuit with an initial condition is shown below. The toggle switch is closed at t= 0. Assuming that a current i(t) flows clockwise in the circuit, Write the integral equation that governs the behavior ofthe circuitcurrent and solve it for the current in the circuit i(t) andvoltage across the capacitor as a function of time using Laplace transforms.Note the polarity of the initial condition as marked in the figure.(Take help fromthe document "Solving RC, RLC,and RLCircuits Using Laplace Transforms" (located in Doc Sharing) and the Week 2 Lecture to see how initial conditions are entered in Laplace domain.)
Make use of the following Laplace transform pair:
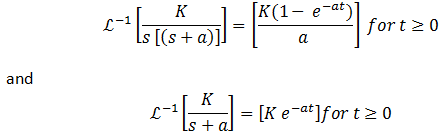
The voltage in a circuit, expressed inLaplace domain, is given by the questions below.
a.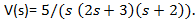 
Find v(t) by first performing a partial fraction expansion and then inverting back to time domain using Laplace tables.
b. Determine the numerical value of v(t) at t= 1second.
c. The voltage in a circuit, expressed inLaplace domain, is given by V(s)= 5/(s2 + 2s + 5).Find v(t) using Laplace tables.
d. Determine the numerical value of v(t) at t= 1 second.
An RLC circuit is shown below. There is an initial voltage of 5 V on the capacitor, with polarity as marked in the circuit. The switch is closed at t= 0 and a current i(t) is assumed to flow clockwise. Write the integral-differential equation of this circuit using Kirchoff'smethod (sum of all voltages around a loop is zero).Apply Laplace transform as outlined in the lecture for Week 2 and in the document "Solving RC,RLC, and RLCircuits Using Laplace Transforms" (located in Doc Sharing) andwrite i(s) in Laplace transform notation. Express the denominator with the coefficient of the highest power of s unity.Then invert to obtain the current in time domain, i(t).
If needed, use the transform pair
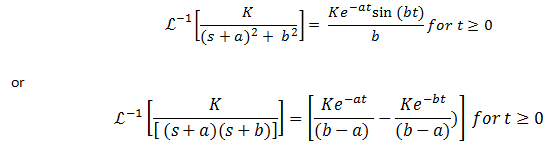
Use whichever is applicable.
|
Slope and intercept in real life
: Need to provide a real world situation where the slope and intercept have some meaning in reality. The situation needs to describe what the dependent and independent variables are and what the slope and intercept means in terms of the real paramet..
|
|
Solve numerical analysis and root finding
: Describe the first iteration--i.e. write down the formula for the next point x2 and the decision that has to be made. Solve Numerical Analysis and Root Finding
|
|
Calculate the dollar sales volume necessary to break-even
: As part of its cost accounting routine, Wilcox Company assigns $36,000 in fixed costs to each product each month. Calculate the break-even dollar sales volume for each project.
|
|
Consolidated financial statements of a us parent
: Are you familiar with any foreign income tax planning strategies that are utilized by some multinational corporations? Do you know of any of the intricacies of how foreign income taxes impact the consolidated financial statements of a US parent?
|
|
Determine the impedances of elements in laplace domain
: Redraw the schematics with the impedance of each of the element shown in Laplace domain. Then determine the overall impedance of the entire circuit between the two ends of the shown circuit and express it in Laplace domain as a ratio of two polyno..
|
|
Plot graph of equations
: Plot the graph of the equations 4x - 6y = 12 and x - 5y = 10 and interpret the result. Plot the graph of the equations 8x - 4y = 12 and -4x + 2y = -6 and interpret the result.
|
|
Compute the break-even point in dollars and in units
: In August, Gold Company sold 770 units of their only product. For the month, fixed costs were $10,400, variable costs were 57% of sales, and the average sales price was $62.
|
|
Gain or income recognizing the exchanges
: What gain or income do Sara and Jane recognize on the exchanges? What is Wren corporation's basis in the property transferred by Sara and Jane? How does wren treat the value of the services Jane renders?
|
|
Equation of the trend line
: Write the equation of the trend line. Do the scores support an increasing or a decreasing trend?
|