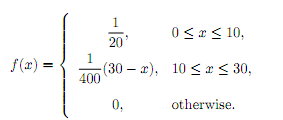Reference no: EM13738974

Question 1.

A local appliance repair store routinely service refrigerators, washing machines, and microwaves. Currently there are two staff members, Adam and Jamie, that handle repairs in the store. Both Adam and Jamie are able to repair washing machines but only Adam can repair refrigerators and only Jamie can repair microwaves.

Service requests arrive at the store with the inter-arrival time distribution:

Time (days)	1	2	3	5	10
Probability	0.42	0.32	0.15	0.10	0.01

Table 1: Interarrival times

The type of appliance to be repaired is equally likely to be a refrigerator, a washing machine or a microwave.

Service requests for appliances will be assigned to the relevant repairperson or, if they are busy, will join the queue for that repairperson. Service requests for refrigerators will be assigned to Adam and service requests for microwaves will be assigned to Jamie. Service requests for washing machines will be assigned to the repairperson with the least number of repair jobs waiting in their queue. In the event of a tie the repair job will be assigned to Adam. Once assigned a repairperson, an appliance will not be reassigned to another repairperson.

The time to finish repairing each appliance is uniformly distributed however its lower and upper limits depends upon the type of the appliance. These lower and upper limits for the uniform distribution are specified in the following table e.g. the microwave repair time is uniformly distributed between 1 and 6 days.

Appliance Type	Refrigerator	Washing Machine	Microwave
Repair time (days)	between 2 and 7	between 3 and 8	between 1 and 6

Determine the average waiting time an appliance spends in the queue and the system during a simulation run of 60 days Give these averages separately for each repairperson and for the store as a whole.

The appliance type is generated from a 1-digit random number (0 being discarded) 1{3 for a refrigerator, 4{6 for a washing machine, and 7{9 for a microwave using the 1st row (from the beginning) of TABLE 5 (the random digits on p. 1157, Winston 4th ed., or on p.

1196, Winston 3rd ed.). Inter-arrival times are generated from 2-digit random numbers starting from 10th (then 11th, 12th, . . . ) row of TABLE 5.

The repair time is generated from a 2-digit random numbers starting from the 20th (then 21st, 22nd, . . . ) row of TABLE 5. You should generate the repair time at the time of the appliance enters service.

In the event of a tie between arrival and departure times process the departures first.

Question 2.

Oswald Industries is planning their buying policy for a 4-month period. It manufactures crankcases for a large auto manufacturer and it buys its raw steel in lot sizes of 100, 200 300, 400 and 500 kg. However, quantity discounts apply, so that

100 kg costs $2 000,
200 kg costs $2 800,
300 kg costs $3 100,
400 kg costs $3 400, and
500 kg costs $3 500:

Anticipated usage over the 4-month period is as follows:

Month	1	2	3	4
Usage (kg)	100	400	200	100

An inventory holding charge of two dollars per kg is incurred per month based on the end of-month inventory including month 4. Shortages are also allowed but are limited to 100kg per month and are charged at fifteen dollars per kg based on the end-of-month inventory which also includes month 4.

The company's storage space will only handle 500 kg at a time. There is no steel in storage at the start of the planning period, and steel used in month of purchase need not be stored.

Determine the how much steel should be ordered each month to minimize the total cost of buying and storing steel to meet the anticipated usage by using dynamic programming.

Question 3.

Howard and Raj are taking turns playing Rock-Paper-Scissors-Lizard-Spock against Shel-don.

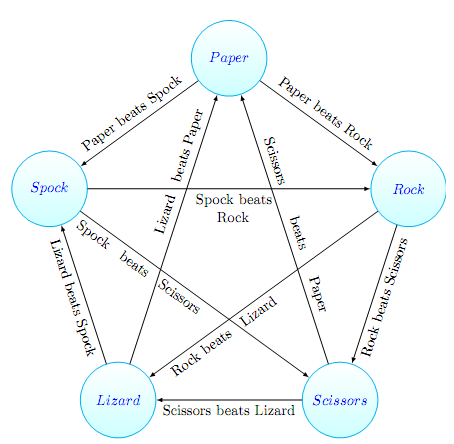
In this game, two players randomly choose one of the five options (Rock, Paper, Scissors, Lizard, or Spock) and reveal their result at the same time. The winner is the player who has the better choice. The following figure shows which choices that beat other choices.

The arrow points to the choices which lose to the starting choice. For instance Rock beats Scissors and Lizard whilst Spock beats Scissors and Rock. If the same choice is chosen by both players, both players continue taking turns until a winner for the game is found.

When playing Sheldon employs a random approach to picking his choices. The probabilities of each choice is given in Table 3.

Sheldon's Choice Rock Paper Scissors Lizard Spock Probability          0.2           0.2           0.2                             0.2        0.2

Table 3: Sheldon's Choices

Raj on the other hand uses a strategy where he picks one of the two choices that would beat the other player's last choice. Although he does favour the traditional Rock{Paper{ Scissors and so will choose the traditional choice of the two with a 0.8 probability and the non-traditional choice (Spock or Lizard) with probability 0.2. In the case Sheldon chose Lizard in the last turn, Raj will choose Scissors with probability 0.8 or Rock otherwise in his next turn.

Howard has the reverse strategy - he picks one of the two choices that would lose to the other player's last choice. He though will choose the traditional choice with 0.5 probability and the non-traditional choice otherwise. In the case Sheldon chose Spock in the last turn, Howard will choose Scissors with probability 0.5 or Rock otherwise.

Raj's and Howard's traditional (or first) choice and non-traditional (or second) choice, given Sheldon's last choice, are summarised in Table 4.

Sheldon's Choice	Raj's 1st Choice	Raj's 2nd Choice	Howard's 1st Choice	Howard's 2nd Choice
Lizard Paper Rock Scissors Spock	Scissors Scissors Paper Rock Paper	Rock Lizard Spock Spock Lizard	Paper Rock Scissors Paper Scissors	Spock Spock Lizard Lizard Rock

Both Howard and Raj will in the first game, in the absence of knowledge of Sheldon last choice, choose one of the five choices randomly with the same probabilities as Sheldon as in Table 3.

Use simulation to compare the Howard's and Raj's strategies when playing Sheldon. Carry out the simulation for the 20 full games each.

Use the one digit random numbers from the 3rd row of TABLE 5 to determine Sheldon's choice. Use the same set of random numbers for Sheldon's choices for his games against Raj and for his games against Howard.

Use the one digit random numbers from the 6th row (from the beginning) of TABLE 5 to determine Howard's and Raj's choice.

Note: Use the same set of random numbers when investigating both strategies. However,

since Draw's are possible, you may need to use a different number of random numbers for Raj's games and for Howard's games.

Question 4.

Jeremy will be playing three consecutive matches of poker with friends tonight. For money they use $10 chips. For each match, he will have the opportunity to place a bet that he will win, the amount bet can be any number of chips (or none) as he has left after the bets on the preceding matches.

Jeremy expects the diculty of each match to become harder when he has more money before each game. If he has less than or equal to $30, his friends will go easy and so he expects a probability is 0.9 that he will win the match and thus win the amount bet whereas the probability is 0.1 that he will lose the match and thus lose the amount he bet. If he has more than or equal to $70, his friends will be more ruthless and so he will have only a 0.2 probability of winning and 0.8 probability of losing the match. Otherwise if he has between $40 and $60, there will only be a 0.6 probability he will win and a 0.4 probability he will lose.

He will begin with $40 worth of chips (4 chips), and his goal is to have $100 at the end. Because these are friendly matches, he does not want to end up with more than $100. A gentleman's agreement between all playing stipulates that they can only bet enough to reach the target but not anymore. i.e. if a player has $70 he can bet at most $30 and no more. He will bet $0 in subsequent matches once he does reach his target. Therefore he wants to find the optimal betting policy that maximises the probability that he will have exactly $100 after the three matches. Use dynamic programming to solve this problem.

Question 5.

Solve the following problem using continuous dynamic programming:

maxz = x²₁ - 5x₁ + 160x²₂ + 12x₃
st        4x₁ + 2x₂ + 3x₃ ≤ 120
x₁, x₂, x₃ ≥ 0

Question 6.

Generate three random observations from each of the following probability distributions (using 4-digit random numbers).

(a) The distribution whose probability density function is (starting from 5th row of TABLE 5)

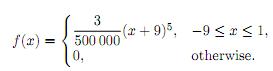
(b) The distribution whose probability density function is (starting from 6th row of TABLE 5)