Reference no: EM131385096
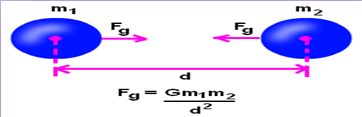
Numerical 01: Determine the force of gravitational attraction between the earth (m = 5.98 x 1024 kg) and a 70-kg physics student if the student is standing at sea level, a distance of 6.38 x 106 m from earth's center.
Numerical 02: Determine the force of gravitational attraction between the earth (m = 5.98 x 1024 kg) and a 70-kg physics student if the student is in an airplane at 40000 feet above earth's surface. This would place the student a distance of 6.39 x 106 m from earth's center(What do you interpret from both the Numerical. State it)
Numerical 03: What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
Numerical 04: Gravitational force on the surface of the moon is only 1/6 as strong as gravitational force on the Earth. What is the weight in newtons of a 10 kg object on the moon and on the Earth?
Numerical 05: Calculate the force of gravitation between the earth and the Sun, given that the mass of the earth = 6 × 1024 kg and of the Sun = 2 × 1030 kg. The average distance between the two is 1.5 × 1011 m.
Numerical 06:
|
Planet
|
Radius (m)
|
Mass (kg)
|
g (m/s2)
|
|
Mercury
|
2.43 x 106
|
3.2 x 1023
|
|
|
Venus
|
6.073 x 106
|
4.88 x1024
|
|
|
Mars
|
3.38 x 106
|
6.42 x 1023
|
|
|
Jupiter
|
6.98 x 107
|
1.901 x 1027
|
|
|
Saturn
|
5.82 x 107
|
5.68 x 1026
|
|
|
Uranus
|
2.35 x 107
|
8.68 x 1025
|
|
|
Neptune
|
2.27 x 107
|
1.03 x 1026
|
|
|
Pluto
|
1.15 x 106
|
1.2 x 1022
|
|
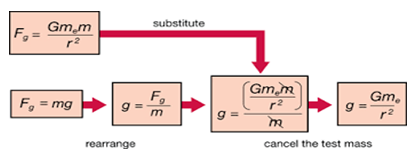
Calculate the value of g in above chart using the formula.
Numerical 07: A stone is released from the top of a tower of height 19.6 m. Calculate its final velocity just before touching the ground.
Numerical 08: A stone is thrown vertically upward with an initial velocity of 40 m/s. Taking g = 10 m/s2, find the maximum height reached by the stone. What is the net displacement and the total distance covered by the stone?
Numerical 09: A car of mass 200 kg moving at 36 km/h is brought to rest after it covered a distance of 10 m. Find the retarding force acting on the car.
Numerical 10: What will be the change in acceleration of a sliding block, if its mass is doubled while a constant force is acting on it?