Reference no: EM13208125

Question 1

The following table shows monthly closing prices in dollars for four of Australia's major stocks. These stocks are BHP Billiton, QBE Insurance, Wesfarmers, and Woolworths. There were no dividends paid by any of these companies during this period.

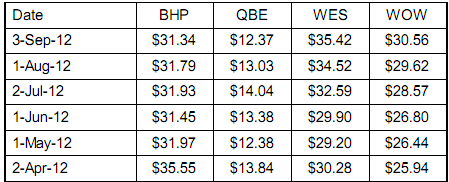
If you use an Excel spreadsheet to help with this question, please show your method of calculation here and list all final numbers, then insert the spreadsheet as the next page.

(a) Determine the monthly historical returns for each of these stocks.

(b) Determine the expected monthly return for each stock if they follow their historical returns.

(c) Determine the monthly volatility of each stock if they continue as per this sample.

(d) Plot the four stocks on a risk-return diagram. Label each stock with its stock code.

(e) Which stock appears the best investment based on past performance, and why?

Question 2

Stock AAA has an expected return of 10% per annum and volatility of 25% per annum. Corporate bond BBB has an expected return of 5% with volatility of 3%. You decide to invest 20% of your funds in stock AAA and 80% in the bond BBB. There is no tax.

(a) If the bond return is completely independent of the stock return, what would be your overall expected return and volatility?

(b) Alternatively if bond BBB is related to company AAA and has a return that appears perfectly correlated with AAA's return, what would be your overall expected return and volatility?

Question 3

National Australia Bank is listed on the Australian Securities Exchange with code NAB. The company has 2.2731 billion shares outstanding and the closing price on 7 Sept 2012 was $25.06.

It is expected to pay dividends of $1.80 per share this year (it has already paid $0.90 in the first half) and in this question you can assume this rate of dividend will continue for ever.

NAB has also issued a variety of debt instruments including some that are listed. One such listing is NABHA, a perpetual floating rate note that pays quarterly interest based on $100 face value. The latest interest rate effective from 15 May 2012 is 5.02% and you can assume in this question this rate stays constant for ever (although in practice a new rate is announced every three months for the following quarter). NABHA had a closing price of $68.00 per note on 7 Sept 2012.

The corporate tax rate in Australia is 30% but National Australia Bank organises its tax affairs well and it has reported its effective tax rate was 22.4% at September 2011.

(a) What is the cost of capital to National Australia Bank of its ordinary shares? 

(b) What is the cost of capital to National Australia Bank of its NABHA floating rate notes?

(c) Imagine NABHA is National Australia Bank's only source of debt funding and suppose there are 100 million of these notes outstanding (neither is true but this simplifies the calculations). In this case what would be the weighted average cost of capital?

Question 4

Jennifer has $100,000 in savings. She borrows a further $50,000 from her bank at 5% interest and invests all $150,000 in a broad portfolio of stocks that approximates the market portfolio. The market is expected to return 12% per annum. Assume borrowing and lending rates are identical.

(a) From the financial figures, determine her expected income from her investment before and after interest expenses, and hence calculate her expected return.

(b) Determine her portfolio beta and hence calculate her expected return using the CAPM equation. Your answer here for her expected return should match that of part (a).

(c) If the market volatility (the standard deviation of the market return) is 20% per annum, what will be the expected volatility of Jennifer's portfolio?

(d) Suppose Jennifer wants an expected return of 18% per annum. What should she do?

Question 5

XYZ Corporation has a very stable business and makes a profit of $1M every year after tax. This never grows nor diminishes, and there is no inflation. For many years XYZ has been paying out all its profits as dividends. At the current share price of $10 and with 1 million shares outstanding, this represents a 10% return. The company has no debt.

The company decides it will change strategy. From now on it will use 20% of its annual profits to buy back as many of its outstanding shares as it can, and it will pay the rest out as dividends. Each year it will buy back the appropriate number of shares and cancel these from its list, then divide the dividend amongst the remaining shares. You can assume there is no systematic risk. Nothing influences the share price besides the information here.

Determine how many shares XYZ should have outstanding after four years of the new strategy, and also the expected value of the fourth dividend. Hint: Build a table that shows what happens each year, step by step (share price before buy back, after buy back, after dividend, etc). Check your work is correct by verifying the IRR of the dividend stream from the new strategy will give the same 10% as would have been expected to be received if you bought for $10 now and had the $1 dividends for ever. Alternatively the valuation under the Gordon model should still be $10.