Reference no: EM1374431
1) Solve the initial value problem
dx/dt = -2x+4,x(0)=5.
Sketch the solution.
2) Solve the initial value problem d2x/dt2 + dx/dt - 6x = 0, x(0) = 1, x'(0) = 1.
3) Solve
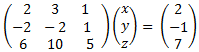
Using Gaussian elimination. Show the steps and write your answer in parametric form.
4) Determine the eigen values and corresponding eigen vectors of

5) Verify that (1,0) is one of the critical points for the nonlinear system
x'=y-x2 + 1
y'=-x-y+1
What is the other critical point? Use the linearized system at (1,0) to determine the stability of (1,0) for the nonlinear system.
1) Assume you are standing at the edge of a 30 meter building and throwa0.2kg ball upward with velocity 20m/second. If the air resistance is providing a force whose magnitude is 0.04 times the speed of the ball, then determine the maximum height of the ball (use g=9.8 in the setup) and the length of time the ball is in the air.
2) Solve the spring mass equation
2x''+2x'+3x=0, x(0)=0,x'(0)=1
For x. How many times will the mass cross equilibrium in the time interval [0,6]?
3)
Using the origin as the initial guess, find the first three iterations of the Gauss-Seidel method when solving
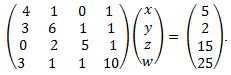
Check the eigen value condition to make sure convergence is guaranteed.
4) First verify that (1,1) is a critical point of the fi order system
x'= x(2-x-y)
y' = y(5-2x-3y)
Next determine the stability of the critical point for both the linearized and nonlinear system using the linearization process (that is, explicitly writed own the linearized system at (1,1) and use the eigen values of the corresponding coefficient matrix).
5) First verify that (2,1) is a critical point for the first order system
x' = 3x-3xy.
y' = -2y+xy
Next determine the linearized system at(2,1)and show that (2,1)is a stable(but not asymptotically stable) critical point for the linearized system. Finally by using the numerical solver in NumSysDE.xmcd to sketch a few trajectories of the nonlinear system starting near (2,1), you should be able to determine the stability of the critical point for the nonlinear system.
|
Question based on marginal revenue
: In short run, assume that all the costs [except film rental and concessions] at a theater are fixed, and that each theater can seat five hundred people per day, no more.
|
|
Supply and demand curves
: During the 4th-quarter of 1993, real GDP in US increase at an yearly rate of over 7 %. During 1994, the economy continued to expand with modest inflation
|
|
Money creation and monetary policy
: You have been employed to manage a small manufacturing facility which has cost and production data given in the table listed below.
|
|
Determine the firm output and price
: Under patent protection, a company has a monopoly in the production of a high tech component. Market demand is estimated to be: P = 100 - 0.2Q.
|
|
Determine the eigen values and corresponding eigen vectors
: determine the stability of the critical point for both the linearized and nonlinear system using the linearization process (that is, explicitly writed own the linearized system at (1,1) and use the eigen values of the corresponding coefficient mat..
|
|
Equilibrium price and quantity after the shift of the supply
: The demand and supply curves for T-shirts in LA, Ca, are given through the following equations, Determine the equilibrium price and quantity after the shift of the demand curve.
|
|
Cost curves in perfect competition industry
: Catfish farming in Louisiana is a perfect competition market. Hence, customers of catfish are getting their catfish at the minimum cost per unit of manufacturing catfish, and they are very happy.
|
|
Use a diagram to show demand curve and marginal revenue
: Northern Granite Corporation, a corporation in New England, installs granite counter tops in houses. When it 1st entered the business, price per foot for installing a granite counter top was $180 per square foot,
|
|
Find the price and quantity for maximum sales revenue
: The market demand function of a company is given by 8P + Q - 64 = 0, and the company's average cost function takes the form AC = 8/Q + 6 - 0.4Q + 0.08Q2.
|