Reference no: EM13495450 , Length: 20

Real Communications Channels

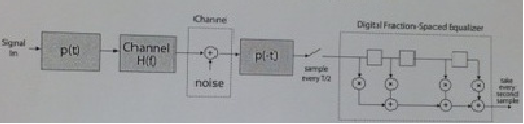
Many practical channels are not distortionless, and we need to "equalize" the channel as discussed in class. The figure below shows the figure from Page 25, but we have added a root-Nyquist transmit and receive filter with, say, a = 1.

This transmission system with the equalizer is shown here:

1) What is the bandwidth over which you need to equalize the channel? De­termine the delay of the delay elements.

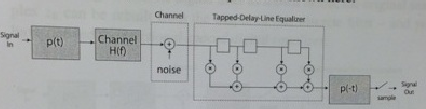
2) Show formally that the receive filter and the tapped-delay line can be interchanged, as shown below, and we can work with this system.What are the delays in the delay elements such that the entire bandwidth of the system is covered. Note that the bandwidth of p(t) is 1 /T.

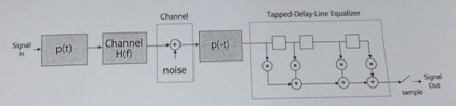
3) Let z(t) be the output of the receiver system. Sample the output at the symbol rate to generate the samples z_k = z(kt).

Now, instead of sampling after the tapped delay line, you sample the sign al at the output of p(-t), but sample it at the Nyquist rate, not the symbol rate. Denote these samples by yj.

Write down an expression for y_i, and show that if these samples are passed through a discrete digital filter a; shown below, the original sam­ples z_k can be rebuilt from the output of this discrete filter - and you have derived the fractional-spaced digital equalizer.