Reference no: EM13836875

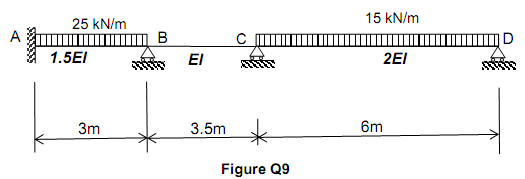
3-PINNED ARCH

Question:

Determine the normal force, shear force and bending moment at point D for the 3-pinned arch shown in Figure and subjected to uniformly distributed load of 50 kN/m between C and B. The arch is pinned at A, B and C and is parabolic in shape (y=ax² with C is the origin).

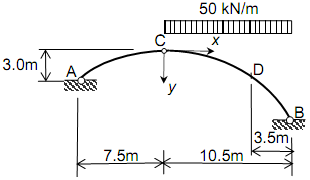
STRAIN ENERGY METHOD

Question

For the statically determinate truss shown in Figure, determine the deflection at C using the strain energy method.

A=1500mm²

E = 200 kN/mm²

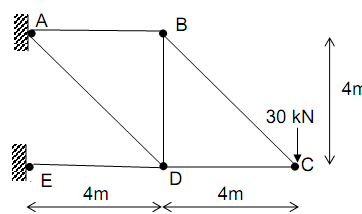
DOUBLE INTEGRATION METHOD (Macaulay)

Question

Figure Q shows a beam subjected to a distributed load which varies linearly in intensity (from zero at support A to 10kN/m at support B). There is no loading on the cantilever part BC.

- Using the double integration (Macaulay) method, derive an expression for the deflection equation along the span AB.

- Determine the deflection at C

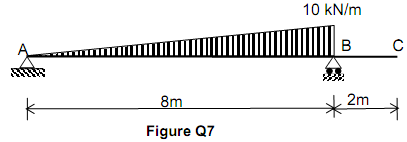
MOMENT AREA METHOD

Question 

Using the moment area moment, determine the deflection at the free end C for the beam shown in Figure.

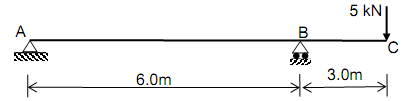
SLOPE-DEFLECTION METHOD

Question 

Use the slope-deflection method to calculate the support reactions and internal force diagrams of the portal frame shown in Figure.

Check the accuracy of the results of the computational model.

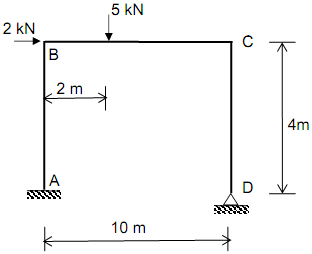
MOMENT DISTRIBUTION

Question 

Figure shows a continuous beam subjected to a uniformely distributed loads along the spans AB and CD. The support C settles by 4mm (vertically downwards).

- Determine the support moments using the moment distribution method.
- Plot the shear force and bending moment diagrams showing key values.