Reference no: EM13802410

Problem 1:

Two bolts are used to form a joint connecting rectangular bars in tension, as shown in Fig. 1. If the bolts have a diameter of 3/8 in., and the load is P = 20 kips, determine the average shear stress on the bolt surfaces that are subjected to direct shear.

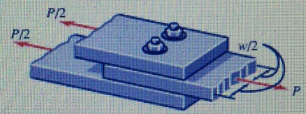
Problem 2:

Two bolts are used to form a joint connecting. rectangular bars in tension, as shown in Fig 1. Determine the required diameter of the bolts if the avci age shear stress for the bolts is not to 12 weed 140 NIPa for the given loading of P = 80 kN.

Problem 3:

A pipe flange is attached by four bolts, whose effective diameter is 0.425 in, to a concrete base. The bolts are uniformly spaced around an 8-in-diameter bolt circle, as shown in Fig.2. If a twisting couple T = 50(10 lb in. is applied to the pipe flange, as shown in Fig. 2, what is the average shear stress in each of the four bolts? Neglect friction between the pipe flange and the concrete base.

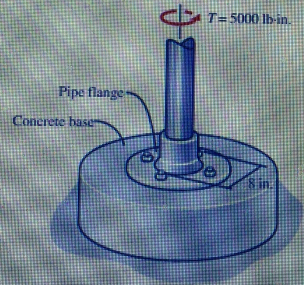
Problem 4:

Two 3/4 in nylon rods are spliced together by gluing a 2-in. section of plastic pipe over the rod ends, as shown in Fig.3. If a tensile force of P = 500 lb is applied to the spliced nylon rod, what is the average shear stress in the glue joint between the pipe and the rods?

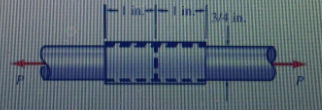
Problem 5:

The forestay (cable) on a sailboat is attached to a tee-bracket on the deck of the boat by a (removable) stainless steel pin. If the allowable shear stress in the pin is Τ_allow = 11 ksi, and the diameter of the pin is dp = 0.25 in., what is the allowable tensile force, T_allow in the stay?

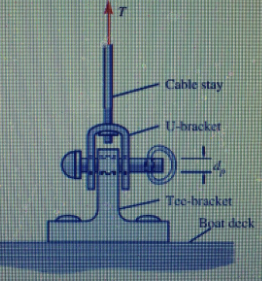
Problem 6:

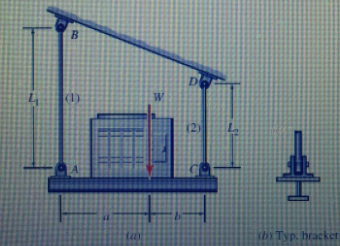
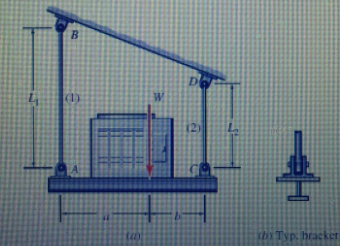
A compressor of weight W is suspended from a sloping ceiling beam by long rods AB and CD of diameters dj and d2, respectively; as shown in Fig.4. A typical bracket is shown in fig.4. Using the data given below, determine the allowable compressor weight, W_allow (Neglect the weight of the platform between A and C, and neglect the weight of the two rods. Also, assume that rod AB and the pins at A and B are large enough that they do not need to be considered.)

Problem 7:

A bar with rectangular cams section is subjected to an axial tensile load P, as shown in Fig. 5 Determine the angle, call it θ_nbT of the plane NN' on which Tnt = 2σ_n, that is, the plane on which the magnitude of the shear stress is twice the magnitude of the normal stress. (b) Determine the angle, call it θ_nbT, of the plane on which σ_n = 2T_m.

Problem 8:

Either a finger-joint splice, Fig. or a diagonal lap-joint splice, Fig., may be used to glue two wood strips together to form a longer tension member. Determine the ratio of allowable loads, (P_f)allow/ (P_d)allow for the following two glue-strength cases:

(a) the glue is twice as strong in tension as it is in shear, that is T_allow = 0.5 σ_allow and (b) the glue is twice as strong in shear as it is in tension, that is ran = 2σ_allow.

Problem 9:

At room temperature (70°F) and with no axial load (P = 0) the extensional strain of the prismatic bar in the axial direction is zero, that is e = 0. Subsequently, the bar is heated to 12.0°F and a tensile load P is applied. The material properties for the bar are: E = 10 x 10³ ksi and a = 13 x 10-"PF, and the cross-sectional area of the bar is IS in2. For the latter load-temperature condi¬tion, the extensional strain is found to be ex = 9(10 x 10-3.

(a) Determine the value of the axial tensile load P. (b) De¬termine the normal stress and the shear stress on the oblique plane NN'. (Note: The total strain is the sum of strain axso¬dated with normal stress a, (Eq. 2.14) and the strain due to change of temperature AT (Eq. 2.8).)

Problem 10:

The thin, rectangular plate ABCD shown in Fig. a undergoes uniform stretching in the x direction,

so that it is elongated by an amount S. Determine an expres¬sion for the (uniform) extensional strain en of the diagonal AC Express your answer in terms of 6. L. and the angle O. Assume that S << 1. and see Appendix A.2 for relevant approximations.

Problem 11:

A rectangular plate ABCD with base h and height It is uniformly stretched an amount Si in the x direction and 5, in the y direction to become the enlarged rectangle A B*C*D* shown in Fig. Determine an expression for the (uniform) extensional strain en of the diagonal AC. Express your answer in terms of δ_x, δ_y, L, and θ, where L = √b²+h² and tanθ = h/b. Base your calculations on the small-displacement assumptions that is δ_x << L assume that δ_y << L.