Reference no: EM13811013
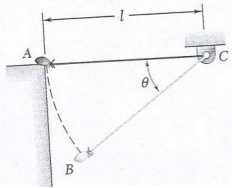
1) A bag is gently pushed off the top of a wall at A and swings in a vertical plane at the end of a rope of length 1. Determine the angle θ for which the rope will break, knowing that it can withstand a maximum tension equal to twice the weight of the bag.
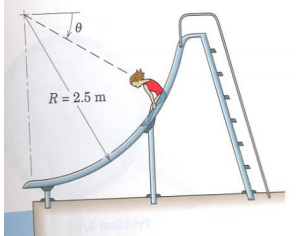
2) Beginning from rest when θ =15°, a 35-kg child slides with negligible friction down the sliding board which is in the shape of a 2.5-m circular arc. Determine the tangential acceleration and speed of the child, and the normal force exerted on her (a) when 0=30° (b) 8=90°
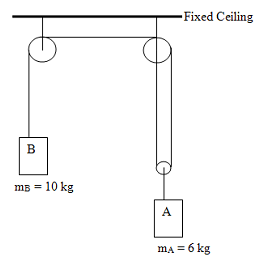
3) Determine the tension in the cables and accelerations of block A and B. Take g = 10 m/s2
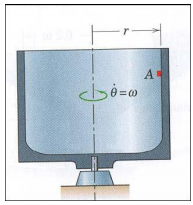
4) A small object A is held against the vertical side of the rotating cylindrical container of radius r. If the coefficient of static friction between the object and the container is μs, determine the minimum angular velocity ω of the container which will keep the object from slipping down the vertical side.
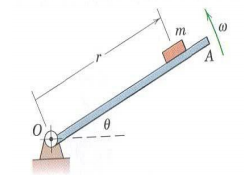
5) The member OA rotates about the horizontal axis through 0 with a constant counterclockwise angular velocity to ω = 3 rad/sec As it passes the position θ = 0, a small block of mass 0.1 kg is placed on it at a radial distance r = 18 inches. If the block is observed to slip at θ = 50°, determine the coefficient of static friction ps between the block and the member.
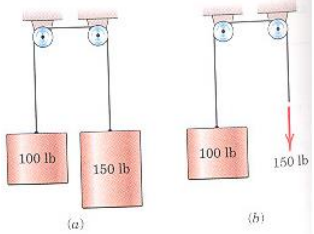
6) Calculate the acceleration of the 100-lb cylinder for each of the two cases illustrated. Neglect friction and mass of pulleys. Note lb here is unit of force. (Take g = 32.2 ft/s2)
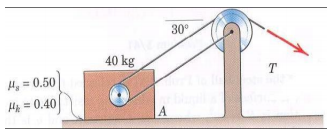
7) Find the minimum value of T (i.e. Tmin) for which the block shown in the figure will start to slip. Next, assume T = 2Tmin and compute the acceleration of the block.
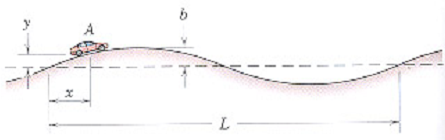
8) A stretch of highway includes a succession of evenly spaced dips and humps, the contour of which is approximately given by y = bsin(2Πx/L) quite probable in San Francisco]. What is the maximum speed at which the car A can go over a hump and still maintain contact with the mad? If the car maintains this critical speed, what is the normal force that it experiences from the ground at the bottom of a dip? The mass of the car is m.
9) The small cart is nudged with negligible initial speed from its horizontal position at A onto the parabolic path, which lies in a vertical plane. Neglect friction.
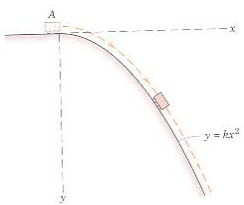
a) Find the expression of the normal force N as a function x
b) Show that N is always > 0 for all values of k.
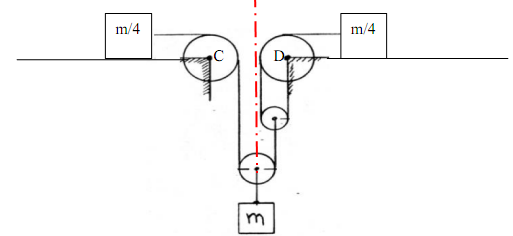
10) For the pulley system shown, find the acceleration of the load m and the tension in the cables. Assume frictionless surfaces, massless pulleys and inextensible cables. The pulleys C and D are at the same level.