Reference no: EM133030634

Question 1. Fluid Mechanics

Derive the result (D) on page CN 12.1-8 of the Boundary Layer notes which is the approximate equation for u(y) in the boundary layer. Show all the steps.

u/u∞ = 3/2(y/δ) - ½( y/δ)3 -D

Question 2. Applied Thermodynamics
Steam enters a turbine at pressure of 3000 kPa and 300 °C and leaves at 50 kPa and 150° C. the turbine mass flow rate is 5 kg/s, inlet velocity is 100 m/s, exit velocity is 60 m/s, heat loss from the turbine is 80 kW. Determine power developed by the turbine.

Question 3. Basic Thermodynamics
A rigid 10-L vessel initially contains a mixture of liquid water and vapor at 120°C with 13.2 percent quality. The mixture is then heated until its temperature is 160°C . Calculate heat transfer required for this process.

Question 4. Power Plant Engineering
Air enter the compressor of a combined gas turbine-vapor power plant at 1 bar, 25°C. The isentropic compressor pressure ratio is 14. The air passing through the combustor receives energy by heat transfer at a rate of 50 MW with no significant decrease in pressure. At the inlet to the turbine the air is at 1250°C. The air expands through the turbine, which has an isentropic efficiency of 87% to a pressure of 1 bar. Then the air passes through the interconnecting heat exchanger and is finally discharged at 200°C, 1 bar. Steam enters the turbine of the vapor cycle at 12.5 MPa, 500°C and expands to a condenser pressure of 0.1 bar. The turbine and pump have isentropic efficiencies of 90 and 100%, respectively. Cooling water enters the condenser at 20°C and exits at 35°C. Determine

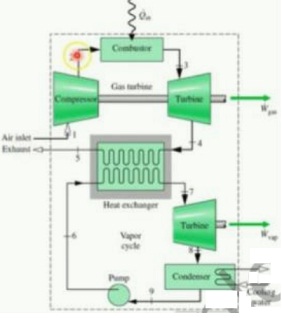
a) the mass flow rates of air, steam, and cooling water, each in kg/s.
b) the net power developed by the gas turbine cycle and the vapor cycle, respectively, each in MW.
c) the thermal efficiency of the combined cycle.

Question 5. Refrigeration and Air conditioning (RAC)

Given a vapour-compression refrigeration cycle with R-410a as the working fluid in the figure below

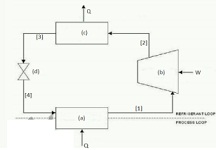
3.1 Indicate whether the heat transfer at (a) and (c) is positive or negative.
3.2 Identity the thermodynamic devises in the cycle, and describe the process in 1, 2, 3, and 4.
3.3 Determine the specific volume v for R-410a at the following states:
T = -15°C; P = 500 kPa
T = 20°C; P = 1000 kPa
T = 20°C; quality 25%

Question 6. Heat transfer

 

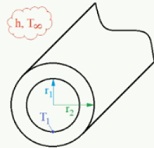
A lens pipe carries hot water and loses heat by convection to the surrounding air at T∞. =18 °C and h-20 W/m2°C). The pipe has a thermal conductivity of k-1.8W/(m°C), inner radius of r1=0 2 in and outer radius of r2=0.23 m. Assume that the inner surface temperature of pipe is T1-56°C if there is no heat generation in the pipe material. calculate the outer surface temperature of the pipe T (r2). in °C. by considering steady one-dimensional heat transfer and constant thermal conductivity.

Question 7. Hydraulic Machines (Pump/ turbines)
The performance data of a water pump follow the curve fit, Havailable = H0-a∀2, where the pump's shutoff head H0= .5.30 m, coefficient a = 1XY 0.8 m(L/s)2. The pump is used to pump watt from one large reservoir to another large reservoir at a higher elevation, both having (roe surfaces open to atmosphere. The system curve simplifies to, Hrequired = (z2-Z1)+ b∀2. where elevation difference is 3.52 m, and coefficient b =93.96 m/(L/s)=. Calculate the operating point of the pump (∀operating and Hoperating ) in appropriate units.

Question 8. Internal Combustion Engine
A gasoline engine can be approximately represented by the idealized cyclic process abc shown in the accompanying diagram of pressure p versus volume V of the gas in the cylinder. Here a - b represents the adiabatic expansion of the air-gasoline mixture, b a c the compression at constant pressure, and c 4 a the final pressurization of the gas at constant volume. Assume this cycle to be carried out quasistatically for a fixed amount of Ideal gas having a constant specific heat. Denote the specific heat ratio by NI = cp/cv . (a) Calculate the pressure at a, expressing your answer in terms of p, v, and y. Hint: p Vconstant is an invariant for an adiabatic process. What's the constant in the exponent? (b) In which process (a 4 b, b 4 c, or c 4 a) the engine takes in heat? (c) Calculate the efficiency q (ratio of work performed to heat intake 01) for this process, expressing your answer in terms of y. Hint: We have derived several expressions for the energy of an ideal gas: E= Cv T= N kB T/y-1 = p V/y-1.