Reference no: EM132353920
Assignment -
Q1. Find the limit of each sequence, or indicate if the sequence is divergent.
(a) an = 1.05n
(b) bn = (2/5)n
(c) cn = (1 + 3/n)n
(d) dn = (1 + 1/n2)n
Q2. Determine if the series is convergent or divergent. Indicate what test you use to make a decision.
(a) n=1∑∞1/√(n+5)
(b) n=1∑∞n/√(n2+1)
(c) n=0∑∞(-1)n 1/(2n+1)
(d) n=1∑∞n(1+n2)-1
(e) n=1∑∞n(1+n2)-2
Q3. (a) Give an example of a conditionally convergent sequence. That is, ∑an is convergent, but ∑|an| is not convergent.
(b) Give an example of an absolutely convergent sequence. That is, both ∑an and ∑|an| are convergent.
Q4. Determine the radius of convergence and the interval of convergence for each of the following power series:
(a) n=1∑∞(-1)n (2n(x-1)n)/n5n
(b) n=1∑∞(-1)n (x+1)n/(3n(n+1)!)
(c) n=0∑∞(5/2 x)n
(d) n=0∑∞(2x)n
(e) n=0∑∞ n(x+2)n/3n
(f) n=0∑∞ ((2n)!xn)/n!
Q5. Determine if the following alternating series are conditionally convergent, absolutely convergent, or divergent.
(a) n=3∑∞(-1)n (ln n)/n
(b) n=2∑∞(-1)n 1/(n ln n)
Q6. Use a regular comparison test, or a limit comparison test, to determine if each of the following series converges or diverges. Indicate which test you are using, and what series is being used for comparison.
(a) n=0∑∞3/(5n+1)
(b) n=0∑∞3/(5n-1)
(c) n=0∑∞1/√(2n+3)
(d) n=1∑∞1/(4n3-3)
(e) n=0∑∞3n/√(2n3+3)
(f) n=0∑∞n2/√(n8+3)
Q7. Test for convergence or divergence:
(a) n=1∑∞(2n)!/n5
(b) n=1∑∞(n/(n+5))n
(c) n=0∑∞1/e√n
(d) n=1∑∞(2+(-1)n)/n1.1
Q8. Express the definite integral 0∫1e-x^2 dx as an infinite series.
Q9. Which function has Maclaurin series n=0∑∞(-1)n 2n xn ? For which values of x is the expansion valid?
Q10. Which function has Taylor series k=0∑∞ ((-1)k/3k+1)(x-3)k? For which values of x is the expansion valid?
Q11. Compute the Taylor polynomial T4(x) centered at a = 3 for the function f(x) = √(x+1). Sketch the graph of f and T4. Compare the values of T4(3.2) and f(3.2).
Q12. Compute the Taylor polynomial T3(x) centered at a = 1 for the function f(x) = ln x. Sketch the graph of f and T3.
Q13. Find an equation of the tangent line to the curve x = ln t, y = t2 + 3t at the point (0, 4) .
Q14. Consider the polar curves r = 4 - 4cos θ and r = 2.
(a) Sketch and shade the region inside of r = 4 - 4cos θ and outside r = 2.
(b) Find the area of the region.
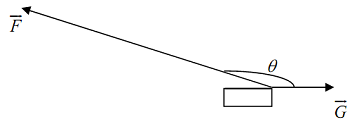
Q15. Determine the magnitude and the direction (relative to G-) of the resultant force (F+G)-. Assume that the angle θ is 160o, and that the magnitudes of F- and G- are |F-| = 150 lbs, |G-| = 15 lbs.
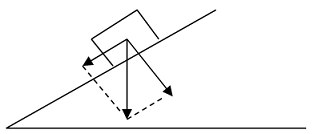
Q16. A block that weighs 150 lbs rests on an inclined plane that makes an angle of 35o with the horizontal. Determine the magnitudes of the components of the weight that are parallel to the plane and perpendicular to the plane.
Q17. Sketch the vectors u→ = (4, 2) and v→ = (-6, 1). Find the angle between these vectors.
Q18. Find the area of the parallelogram determined by u→ = (4, 2, 5) and v→ = (3, -4, 5) in R3. Find the angle between these vectors.