Reference no: EM131110236

2008 Honors Examination in Probability

1. Suppose that you ask a random sample of 36 male students at Swarthmore how many minutes they spend at the gym during a typical workout session. Using their data, you compute a 99% confidence interval for the population average and obtain 25.3 to 50.1 minutes. You also compute the p-value for a one-sided test of the null hypothesis that the population average equals 30 minutes and obtain a p-value of about 0.11. Assume that the data follow a normal curve.

(a) What is the standard deviation for these 36 men?

(b) Below are five statements about the confidence interval and p-value. For each statement, if you believe that it is always true, simply write "true" on your answer sheet. Otherwise, write "false" and explain precisely why the statement could be false in five or fewer sentences.

i. Approximately 99% of all male Swarthmore students work out between 25.3 and 50.1 minutes during a workout.

ii. A 99% confidence interval obtained from a random sample of 100 male Swarthmore students has a better chance of containing the population average than a 99% confidence interval obtained from a random sample of 36 male Swarthmore students.

iii. If we took random samples of 36 male Swarthmore students over and over again, we would expect roughly 99% of the sample averages to fall between 25.3 and 50.1.

iv. There is an 11% chance that the population average equals 30.

v. If the null hypothesis was true, there is an 11% chance that we'd observe a sample average that exceeds 37.7.

2. Suppose that a finite population contains N elements. You take a sample of n elements from this population (how you do so will be described in parts of the problem). Let I_i = 1 if element i is selected in the sample, where i = 1, . . . , N. Let I_ij = 1 if element i and element j are both selected in the sample, where i = 1, . . . , N, j = 1, . . . , N, and i ≠ j. For all i, let the probability that record i is selected be π_i = P(I_i = 1). For all pairs (i, j), let the probability that both records are selected be π_ij = P(I_ij = 1).

(a) Suppose that the sample is selected without replacement.

i. How many distinct samples of n elements are there? Two samples, say S₁ and S₂, are distinct when i ∈ S₁ but i ∉  S₂ for at least one i. Samples with the same elements selected in different orders are not distinct.

ii. Determine π_i for any i.

iii. Determine π_ij for any pair i, j such that i ≠ j.

iv. Suppose that T = a₁I₁ + a₂I₂ + a₃I₃, where a₁, a₂, a₃ are positive constants. Determine V ar(T).

(b) Suppose that the sample is selected with replacement.

i. Determine π_i for any i.

ii. Determine π_ij for any pair i, j such that i ≠ j.

3. Infectious diseases are sometimes modelled with a so called SIR model (the letters stand for Susceptible, Infected, and Recovered). People begin in class S, then possibly migrate to class I (i.e., become infected), and then to class R (i.e., recover); no other transitions are possible. In a simple version of the model, the ith individual begins in class S, waits a random amount of time Ti with an exponential distribution, f(t|λ) = λe^-λt, before migrating to class I, then waits another random amount of time W_i with exponential distribution f(w|µ) = µe-µw, before migrating to class R, with all the exponentially distributed random variables {T_i, W_i} independent.

(a) Let N denote the number of Susceptibles at time 0, and let X_t be the number of these who become infected by time t. Find the probability distribution of X_t.

(b) Let Z₁ be the length of time until the first of those people becomes infected, i.e., Z₁ = min(T₁, . . . , T_N). Find the probability distribution for Z₁.

(c) Let Z_N be the length of time until the last of those people becomes infected, i.e., Z_N = max(T₁, . . . , T_N). Find the probability density function for Z_N.

(d) Let Y_i = T_i + W_i be the total amount of time the ith Susceptible waits before joining class R. Find the probability distribution of Yi under the (simplifying) assumption µ = λ.

4. A commonly used probability distribution for monetary random variables is the Pareto distribution. Assume all values of the random variable are greater than or equal to some baseline value k. The Pareto probability density function is

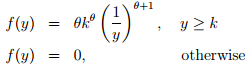
where θ ≥ 1. Assume that k is known and that k > 2.

(a) Determine the expected value of Y.

(b) Determine the probability density function of Z = log(Y ), where log is the natural logarithm.

(c) Determine the expected value of Z.

(d) Let W_n = _i=1∑ⁿ (log(Y_i) - log(k))/n, where {Y₁, . . . , Y_n} are independent samples from f(y). Show that W_n approaches 1/θ as n → ∞.

5. Suppose that you collect data {Y₁, . . . , Y_n} that are independent and identically distributed according to an exponential distribution with parameter λ,

f(y) = λ_e - λ_y,      y ≥ 0

f(y) = 0,                otherwise.

(a) Suppose that Y is the lifetime in minutes for a machine. A certain machine has been working for 3 minutes already. Given this information, find the chance that its total lifetime will be less than 10 minutes. Use λ = 0.2 for part (a) only.

(b) Find the moment generating function of Y.

(c) Use the moment generating function to determine the mean and variance of Y.

(d) What is the approximate distribution of Y¯ = _i=1∑ⁿ Y_i/n as n → ∞?

(e) Suppose that you decide to use Bayesian inference to learn about λ. You use a prior distribution for λ that is also an exponential distribution with parameter equal to µ. Determine the posterior distribution of λ given the observed data and µ.

6. A certain person goes for a run each morning. When he leaves his house for his run he is equally likely to go out either the front or back door; and, similarly, when he returns he is equally likely to go to either the front or back door. The runner owns two pairs of running shoes. After each run, he takes off his shoes at whichever door he happens to be. If there are no shoes at the door from which he leaves, he runs barefoot. We are interested in the proportion of time that he runs barefoot.

(a) Set up a Markov chain to help you learn about the proportion of time that he runs barefoot. Give the states and the transition probabilities.

(b) If he runs barefoot on Monday morning, what is the chance that he will run barefoot on Thursday morning?

(c) Determine the long-run proportion of days that he runs barefoot.