Reference no: EM131081356

Sample final questions-

1. Consider the power series

_n=1∑^∞xⁿ/n³,          _n=1∑^∞x³ⁿ/2n,       _n=0∑^∞x2n!.

For each power series, determine its radius of convergence R. By considering the series at x = ±R, determine the exact interval of convergence.

2. (a) Prove by using the definition of convergence only, without using limit theorems, that if (s_n) is a sequence converging to s, then lim_n→∞ s_n² = s².

(b) Prove by using the definition of continuity, or by using the ε-δ property, that f(x) = x² is a continuous function on R.

3. Let f be a twice differentiable function defined on the closed interval [0, 1]. Suppose r, s, t ∈ [0, 1] are defined so that r < s < t and f(r) = f(s) = f(t) = 0. Prove that there exists an x ∈ (0, 1) such that f''(x) = 0.

4. (a) Suppose that _n=0∑^∞a_n is a convergent series. Define a sequence (b_n) according to b_n = a_2n + a_2n+1 for n ∈ N ∪ {0}. Prove that _n=0∑^∞b_n converges.

(b) Construct an example of a series _n=0∑^∞ a_n that diverges, but that if (b_n) is defined as above, then _n=0∑^∞ b_n converges.

5. Suppose f a is real-valued continuous function on R and that f(a)f(b) < 0 for some a, b ∈ R where a < b. Prove that there exists an x ∈ (a, b) such that f(x) = 0.

6. Let f be a real-valued function defined on an interval [0, b] as

Consider a partition P = {0 = t₀ < t₁ < . . . < t_n = b}. What are the upper and lower Darboux sums U(f , P) and L(f , P)? Is f integrable on [0, b]?

7. Let f be a decreasing function defined on [1, ∞), where f(x) ≥ 0 for all x ∈ [1, ∞). Prove that ₁∫^∞f(x)dx converges if and only if _n=1∑^∞f(n) converges. [This is essentially a question asking you to prove a general form of the integral test.]

8. Consider the function defined for x, y ∈ R as d(x, y) =

(a) Prove that d defines a metric on R.

(b) What is the neighborhood of radius 1/2 centered on 0?

(c) Consider an arbitrary set S ⊆ R. Is S open? Is S compact?

9. Let x = (x₁, x₂) and y = (y₁, y₂) be in R². Consider the function

d(x, y) = |x¹ - y¹| + |x² - y²|.

(a) Prove that d is a metric on R².

(b) Compute and sketch the neighborhood of radius 1 at (0, 0).

10. Consider a function f defined on R which satisfies

|f(x) - f(y)| ≤ (x - y)²

for all x, y ∈ R. Prove that f is a constant function.

11. Suppose that f is differentiable on R, and that 2 ≤ f'(x) ≤ 3 for x ∈ R. If f(0) = 0, prove that 2x ≤ f(x) ≤ 3x for all x ≥ 0.

12. Show that if f is integrable on [a, b], then f is integrable on every interval [c, d] ⊆ [a, b].

13. (a) Suppose r is irrational. Prove that r^1/3 and r + 1 are irrational also.

(b) Prove that (5 +√2)^1/3 + 1 is irrational.

14. By using L'Hopital's rule, or otherwise, evaluate

lim_x→0 (x/1 - e^{-x^2-3x}),     limx→0(1/sin x - 1/x),                   limx→0(x³/sin x - x).

15. Let a ∈ R. Consider the sequence (s_n) defined as

Compute lim sup s_n and lim infs_n. For what value of a does (s_n) converge?

16. Consider the function f: R² → R defined as f(x₁, x₂) = 1/x₁² + x₂² + 1.

With respect to the usual Euclidean metrics on R and R², prove that f is continuous at (0, 0) and at (0, 1).

17. (a) Calculate the improper integral ₀∫¹x^-p dx, for the cases when 0 < p < 1 and p > 1.

(b) Prove that ₀∫^∞x^-p dx = ∞, for all p ∈ (0, ∞).

18. Prove that if f is integrable on [a, b], then lim_{d→b- a}∫^df(x) dx = _a∫^b f(x) dx.

19. Let f(x) = x², and define a sequence (s_n) according to s₁ = λ and s_n+1 = f(s_n) for n ∈ N. Prove that (s_n) converges for λ ∈ [-1, 1], and diverges for |λ| > 1.

20. Consider the three sets

A = [0, √2] ∩ Q,                B = {x² + x - 1: x ∈ R},      C = {x ∈ R: x² + x - 1 < 0}.

For each set, determine its maximum and minimum if they exist. For each set, determine its supremum and infimum. Detailed proofs are not required, but you should justify your answers.

21. Let f_n(x) = x - xⁿ on [0, 1] for n ∈ N.

(a) Prove that f_n converges point-wise to a limit f, and determine f .

(b) Prove that fn does not converge uniformly to f.

(c) Find an interval I contained in [0, 1] on which f_n → f uniformly.

(d) Prove that the f_n are integrable, that f is integrable, and that ₀∫¹f_n → ₀∫¹ f.

22. Define

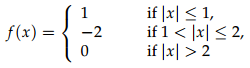
for x ∈ R.

(a) Calculate F(x) = 0∫xf(t)dt for x ∈ R.

(b) Sketch f and F.

(c) Compute F' and state the precise range over which F' exists. You may make use of the second Fundamental Theorem of Calculus.

23. (a) Let f and g be continuous functions on [a, b] such that _a∫^b f = _a∫^b g. Prove that there exists an x ∈ [a, b] such that f(x) = g(x).

(b) Construct an example of integrable functions f and g on [a, b] where _a∫^bf = _a∫^bg but that f(x) ≠ g(x) for all x ∈ [a, b].

24. Define the sequence of functions hn on R according to

 (a) Sketch h₁, h₂, and h₃.

(b) Prove that h_n converges point-wise to 0 on R/{0}. Prove that lim_n→∞ h_n(0) = ∞.

(c) Let f be a continuous real-valued function on R. Prove that lim_{n→∞ -∞}∫^∞h_n f = f(0).

(d) Construct an example of an integrable function g on R where limn→∞_-∞∫^∞h_ng, exists and is a real number, but does not equal g(0).

25. Consider the function f(x) = x/1 + x.

on the interval [0, ∞).

(a) Show that lim_x→∞ f(x) = 1, and that 0 ≤ f(x) < 1 for all x ∈ [0, ∞).

(b) Sketch f.

(c) Calculate f', f'', and use them to construct the partial Taylor series at x = 1 with the form

f_T(x) = _n=0∑²((x - 1)ⁿf⁽ⁿ⁾(1)/n!).

(d) Show that f_T can be written as a quadratic equation with the form ax² + bx + c, and compute a, b, and c.

(e) Add a sketch of f_T to the sketch of f . [Note: f_T(1) = f(1) so the two curves should intersect at x = 1.]

26. Determine the radius of convergence R of the power series

f₁(x) = _n=0∑^∞xⁿ/√(n² + 1),                               f2(x) = _n=1∑^∞(-2)ⁿx²ⁿ/n².

By considering the series at x = ±R, determine the exact intervals of convergence. If you make use of any of the theorems for determining series properties, you should state which ones you use.

27. Suppose (s_n) and (t_n) are two sequences that converge to s and t respectively. State the definition of convergence, and use it to prove carefully that 3s_n + t_n → 3s + t. Do not use the limit theorems for sequences.

28. The Fibonacci numbers are defined by F₀ = 0 and F₁ = 1, and

F_n+1 = F_n + F_n-1

for n ∈ N. Let the golden ratio be defined as ? = 1+√5/2.

(a) Show that ?² = 1 + ?.

(b) Let f(n) = ?ⁿ - (1 - ?)n/√5.

For n ∈ N, define H_n to be the hypothesis that "both F_n = f(n) and F_n-1 = f(n - 1)". Apply mathematical induction to prove that H_n is true for all n ∈ N, and deduce that Fn = f(n) for all n ∈ N ∪ {0}. [Hint: it is simpler to carry out the algebra in terms of ? and use the identity in (a), as opposed to calculating explicitly in terms of (1 + √5)/2.]

(c) Show that F_n+1/F_n → ? as n → ∞.

29. Let f be a continuous strictly increasing function defined on R. Consider a subset S ⊆ R and let T = { f(x) : x ∈ S}.

(a) If sup S is finite, prove that sup T = f(sup S).

(b) Suppose (an) is a sequence such that lim sup a_n is finite. Define the sequence (b_n) so that bn = f(an) for all n. Prove that lim sup b_n = f(lim sup a_n).

(c) Suppose the condition that f is continuous is removed. Construct an example of a strictly increasing function f defined on R, and subset S ⊆ R, where sup S is finite, but sup T ≠ f(sup S).

30. Consider two dimensional space R², where an element x ∈ R² is written as x = (x₁, x₂). Let d_E(x, y) = ((x₁ - y₁)² + (x2 - y2)²)^1/2 be the usual Euclidean metric on R².

(a) Prove that d_A(x, y) = min{|x₁ - y₁|, 2|x₂ - y₂|} is not a metric on R².

(b) Prove that d_B(x, y) = max{|x₁ - y₁|, 2|x₂ - y₂|} is a metric on R². Draw the neighborhood of radius 1 at (0, 0).

(c) Consider an arbitrary metric space (X, d), and a mapping f : X → R². Suppose that f is continuous with respect to (X, d) and (R², dE). Prove that it is also continuous with respect to (X, d) and (R², dB).

31. Consider the function defined on [0, ∞) as

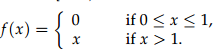
 (a) Compute F(x) = ₀∫^x f(t)dt on [0, ∞).

(b) Calculate F'(x), stating the precise range over which it exists. You may make use of the second Fundamental Theorem of Calculus.

(c) Prove that neither f nor F is uniformly continuous on [0, ∞).

32. Let f(x) = x²(1 - x) and g(x) = | f(x)| for x ∈ R.

(a) Plot f and g.

(b) By using the definition of differentiability, prove that g(x) is differentiable at x = 0, but not at x = 1.

(c) Compute the derivatives g⁽ⁿ⁾(2) for n ∈ N, and use them to write down the Taylor series of g at x = 2. Prove that this series is equal to -f(x) for all x ∈ R.

33. Consider the function defined on the domain [0, ∞) as

Define a sequence of functions on the interval [0, 1] according to f_n(x) = ng(nx) for n ∈ N.

(a) Sketch f₁, f₂, and f₃ on the interval [0, 1].

(b) Prove that f_n converges point-wise to a limit f, and determine f.

(c) Prove that f_n does not converge uniformly to f on [0, 1].

(d) Show that ₀∫¹f_n = 1/2 for all n. Does ₀∫¹f_n converge to ₀∫¹ f?

34. (a) Suppose that f is a differentiable function on (0, ∞), and that f'(x) → 0 as x → ∞. Define g(x) = f(x + 1) - f(x). Use the Mean Value Theorem to prove that g(x) → 0 as x → ∞.

(b) Use the Intermediate Value Theorem to show that for all n ∈ N, the equation p(x) = x²ⁿ⁺¹ - 4x + 1, has at least three real roots. In addition, prove that these roots must be irrational.

35. (a) Use L'Hopital's rule to evaluate

lim_x→0 x/e^x - e^-x,               lim_x→0sin²x/x².

(b) Let f be a real-valued function defined on an interval (a, b). Let x ∈ (a, b), and suppose f is twice differentiable at x. Show that the limit

lim_h→0(f(x + h) + f(x - h) - 2 f(x)/h²)

exists and equals f''(x).

(c) Construct an example of a real-valued function f defined on an interval (a, b), where for some x ∈ (a, b) the above limit exists and is finite, but f is not twice differentiable at x.

36. (a) Let (f_n) be a sequence of integrable functions on [a, b], and suppose that f_n → f uniformly on [a, b]. Prove that f is integrable on [a, b] and that

_a∫^bf = lim_n→∞a∫^b f_n.

(b) By using integration by parts, prove that

_1/2∫¹log x dx = (log 2/2 - ½).

(c) Recall that for |x| < 1,

log(1 + x) = _n=1∑^∞xⁿ(-1)ⁿ⁺¹/n.

By using this and the results from parts (a) and (b), prove that log 2 = 1 - _n=1∑^∞ 1/n(n + 1)2ⁿ.