Reference no: EM132740356

PROBLEM 1:

This is a similar problem of 5.44 in the book (7th edition), however, you are required to draw the shear and bending-moment diagrams based on the method of the left and right end internal force and moment of each section

Draw the shear and bending-moment diagrams for the beam and loading shown. and determine the maximum absolute value (a) of the shear. (b) of the betiding moment.

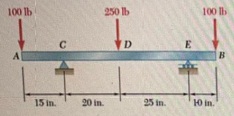
PROBLEM 2:

This is a similar problem of 5.5 in the book (7th edition), however, you are required to draw the shear and bending-moment diagrams based on x function internal force and moment in each section

For the beam and loading shown, (a) draw the shear and bending-moment diagrams. (b) determine the equations of the shear and bending-moment curves.

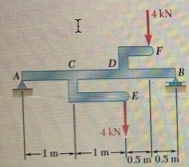
PROBLEM 3:

This is a similar problem of 5.41 in the book (7th edition), however, you are required to draw the shear and bending moment diagrams based on the method of load, shear and bending moment relationship.

Using the method of Sec. 5.2. solve Prob. 5.8.

Draw the shear and bending-moment diagrams for the beam and loading shown. and determine the maximum absolute value (a) of the shear, (b) of the bending moment.

PROBLEM 4:
This is a similar problem of 5.43 in the book (7th edition), however, you are required to draw the shear and bending-moment diagrams based on the method of load, shear and bending moment relationship.

Draw the shear and bending moment diagrams for the beam and loading shown and determine the maximum absolute value (a) of the shear. (b) of the bending moment.

PROBLEM 5:

This is a similar problem of 5.65 in the book (7th edition), when you draw the shear and bending-moment diagrams, you can use anyone you prefer for

For the beam and loading shown. design the cross section of the beam. knowing that the gradl of timber used has an allowable normal stress of 12 MPa.

PROBLEM 6:

This is a similar problem of 5.75 in the book (7th edition), when you draw the shear and bending-moment diagrams, you can use anyone you prefer for.

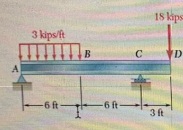
Knowing that the allowable normal stress for the steel used is 24 ksi. select the most economical S-shape beam to support the loading shown.

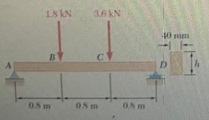
Part 2:

Problem 1:

This is a similar problem of 6.18 in the book (7th edition), when you draw the shear and bending-moment diagrams, you can use anyone you prefer for,

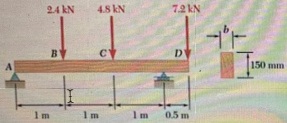
For the beam and loading shown. determine the minimum required width b. knowing that for the grade of timber used. σall =12 MPa and τall =825 kPa.

Problem 2:
This is a similar problem of 6.19 in the book (7th edition), when you draw the shear and bending-moment diagrams, you can use anyone you prefer for.

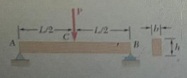
A timber beam AB Of lenght L and rectaungular cross section carries a single concetrated load P at its midpoint C. a) Show that the ratio τ_m/σ_m of the maximum values of the shearing and normal stress in the beam is equal to 2h/L, where h and L are, resepectively. the depth and the lenght of the beam (b) Determine the depth h and the width b of the beam knowing that L = 2m, P = 40kN, τ_m = 960 kPa, and σ_m = 12 mPa.