Reference no: EM131140678

1. What is the domain of f(x) = √(1 - x²) and where is f continuous?

2. State whether the indicated function is continuous at 4.

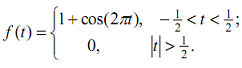
3. Suppose f(x) is defined as shown below.

a. Use the continuity checklist to show that f is not continuous at 0.

b. Is f continuous from the left or right at 0?

c. State the interval(s) of continuity.

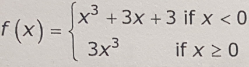
4. Determine the interval(s) on which the following function is continuous. Be sure to consider right- and left-continuity at the endpoints.

f(x) = √(3x² - 24)

5. Evaluate the following limit.

lim_x→3π/2(sin²x + 5 sinx + 4/sin x + 1)

6. Use the Intermediate Value Theorem to verify that the following equation has three solution on the interval (0, 1). Use a graphing utility to find the approximate roots.

140x³ - 139x² + 38x - 3 = 0

7. Check whether the function f(x) = (x² - 11x + 28/x - 5) has a removable discontinuity at the point a = 5.

8. Suppose x lies in the interval (4, 6) with x ≠ 5. Find the smallest positive value of δ such that the inequality 0 < |x - 5|< δ is true for all possible values of x.

9. For the function f(x) = 4x + 7, P(-3, -5):

a. Use the definition m_tan = lim_x→a(f(x) - f(a)/x - a) to find the slope of the line tangent to the graph of f at P.

b. Determine an equation of the tangent line at P.

c. Plot the graph off and the tangent line P.

10. For the function f (x) = 7x + 4, P (0, 4):

a. Use the definition m_tan = lim_h→0(f(a+h) - f(a)/h) to find the slope of the line tangent to the graph of f at P.

b. Determine an equation of the tangent line at P.

11. Let f (x) = (1 / 4+3x) and point p = (1, 1/7).

a. Use the following definitions of the slope of the tangent line at x = a to find the slope of the line tangent to the graph of f at P.

m_tan = lim_h→0(f(a+h) - f(a) / h)

b. Determine an equation of the tangent line at P.

12. For the function and point f(x) = 2/√x, a = 1/9

a. Find f'(a).

b. Determine an equation of the line tangent to the graph of f at (a, f(a)) for the given value of a.

13. Use the graph of g in the figure to do the following.

a. Find the values of x in (-1, 7) at which g is not continuous.

b. Find the values of x in (-1, 7) at which g is not differentiable.

c. Sketch a graph of g'.

14. Find the derivative of the following function.

g(t) = 12√t

15. Find the derivative of the following function.

f(x) = 9x³ + 4x

16. Find the derivative of the following function.

f(x) = 14x³ - 25x + ¼

17. Find the derivative of the following function by first expanding the expression.

f(x) = (6x + 5)(5x² + 7)