Reference no: EM132187179

Applied Elasticity and Plasticity Project -

Use a computer program to draw the yield surfaces of the yield criteria given in the table below (a) on deviatoric planes at ρ = 0 and four other different values, where ρ = I₁/√3 = √3σ_m = √3σ_oct; (b) on meridain planes at θ = 0^o, 15^o, 30^o, 45^o, and 60^o. (c) Also draw the 3-D perspective views of the yield surfaces in the principal-stress space from three different angles.

Yield Criteria	Uniaxial Compressive Yield Stress	Uniaxial Tensile Yield Stress
von Mises	50,000 psi	50,000 psi
Mohr-Coulomb	2,000 psi	200 psi
Yield criterion defined below	2,000 psi	200 psi

The yield surface of the yield criterion is expressed in the form:

F(σ_∼) = √3τ₀ - r(θ, σ₀/σ_yc, k_s) = 0 (1)

where σ_∼ is the stress tensor whose Cartesian components are σ_ij, σ₀ = I₁/3, I₁ = σ_kk = first invariant of stress tensor, τ₀ = √(2J₂/3), J₂ = s_ijs_ij/2 = second invariant of the stress deviator s_ij = σ_ij - 1/3 δ_ijσ_kk, δ_ij = Kronecker delta, θ = 1/3 cos^-1((3√3)/2)J₃J₂^-3/2) = similarity angle which represents the polar angle in the deviatoric section, J₃ = 1/3 s_ijs_jks_ki = third invariant of s_ij, σ_yc is the uniaxial compressive yield stress, k_s is a constant which determines the size of the yield surface, and function r(θ, σ₀/σ_yc, k_s) represents the deviatoric section of the yield surface which can be expressed by the formula

where r_t and r_c represent the tensile and compression meridians, respectively, which are defined as:

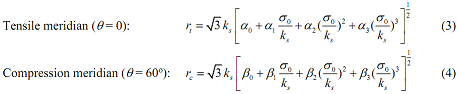
The equations above involve eight parameters α₀, · · ·, α₃, β₀,· · · , β₃. These eight parameters and constant k_s can be determined based on the following conditions:

1. The two apices of each curve of Eq. 3 and Eq. 4 on the horizontal axis must be common to both curves.

2. The point representing the yield stress under uniaxial tension has to be on the yield surface.

3. The point representing the yield stress under uniaxial compression has to be on the yield surface too.

The above conditions are not enough to determine a unique set of the constant values. Use any set of constants fulfill the above conditions for your project. Include a section in your project report to show the values you use and explain and show calculations how you determine the constants.

Note - It has to be done in Matlab. As for the report of 1000 words need Abstract, intro, procedure, discussion of results, conclusion.

Attachment:- Assignment File.rar