Reference no: EM133273316
Question 1. Digital Constellations
A digital modulation scheme consisting of the following four signals is used to communi- cation information over an AWGN channel with power spectral density No/ 2 = 1.
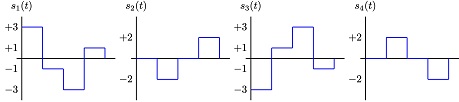
Figure 1: 4-ary modulation signal set
Bits arrive at the digital modulator with an unequal distribution, with bit bk being ‘0' with probability 0.6 and 1' with probability 0.4.
(a) Determine a set of orthonormal basis functions for this modulation scheme and provide the corresponding signal constellation diagram.
(b) Choose a mapping of bits to constellation points that will minimise the average energy per symbol, Es while also giving decent bit error performance. Please explain your thinking in determining this mapping.
(c) Calculate Es based on the mapping you chose in (b).
(d) Determine the MAP decision boundaries for deciding signal s1(I) is sent and clearly mark these on your constellation diagram.
(e) Use the MAP decision boundaries you found in (d) along with the union bound to upper bound the symbol error probability with signal s1(t) is sent, i.e., upper bound P(error|s = s1)
Please list all of the resources you used to answer this question including references to the subject notes, workshops and problem sets as well as any websites or textbooks etc.
Question 2. Communication Design
Consider the baseband 2-PAM communication system of Figure 2 that employs a root raised cosine (RRC) pulse at both the transmit and receive filters. You are to choose parameters for this system to maximise the bit rate under the following constraints.
• Maximum available bandwidth: 1 MHz
• Maximum transmit power: 3 W
• Maximum allowable bit error rate: 10-3
The transmitted signal passes through a benign channel, but the sampling error in the symbol sampling can be up to 20% of the chosen symbol period, Y. This worst case symbol timing error is modelled as a time advance in the channel, c(t) = δ(t + τ), where τ = 0.2T.
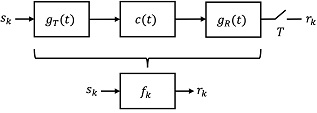
Figure 2: ISI model for 2-PAM receiver.
(a) For now assume that an RRC pulse with β = 0.2 is employed. Determine an equivalent discrete-time ISI model (i.e. determine FIR filter taps fk) to capture the combined effects of gT(t), c(t) gT(t) and the sampling operation. Keep only the five most significant (largest magnitude) taps in your model.
(b) Assume that the received symbols are also corrupted by i.i.d. Gaussian noise,
yk = rk + ηk).
where ηk ~ N(0, N0/2.
Determine an expression to calculate the bit error probability, Pt, under this ISI model when symbol-by-symbol detection is used (no equal- isation) and the decision boundary is set a yk = 0.
(c) Write a MATLAB script that repeats the previous two steps for ten evenly spaced values of Q C 0, 1]. Provide a combined plot of Pt versus E fN for each Q, where At/No 0, 15] dB. Include on your plot a curve for the theoretical performance of binary PAM.
(d) Based on your plots of the previous question, choose values of Q and F to maximise the data rate subject to the original constraints of the problem and assuming No/2 = 10 W/Hz.
Please list all of the resources you used to answer this question including references to the subject notes, workshops and problem sets as well as any websites or textbooks etc.
Question 3. FSK and Non- Coherent Receivers
Consider a system using binary Frequency Shift-Keying (FSK) to send information over an AWGN channel. On the symbol interval 0, F), the possible transmitted symbols are:
s1(t) = √EbΦ1(t) and s2(t) = √EbΦ1(t) where
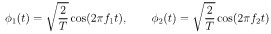
with T = 2 ms and f1 = fc - fΔ, f2 = fc + fΔ, fc = 5 MHz, fΔ = 250 Hz.
(a) Prove that Φ1(t) and Φ2(t) are orthonormal.
(b) Assume the received signal is r(t) = √2Eb/T.cos(2Πfmt) + n(t) where m ∈ (1, 2} and n(t) is white Gaussian noise with power spectral density N0/2. The optimal receiver first correlates the received signal with Φ1(t) and Φ2(t) to produce r1 = [r(t), Φ1(t) and r2 = (r(t), Φ2(t)). The detector then selects so if r1 > r2 otherwise it selects s2.
Determine the conditional joint pdf of and r1 > r2 given sm was sent, p(r1, r2|sm). m ∈ (1, 2} and then determine the bit error probability as a function of Eb/No
(c) Now suppose that the received signal is r(t) = √2Eb/T.cos(2Πfmt) + θ for some unknown θ. Assuming the same receiver as in (b), determine an expression for the conditional joint pdf of r1 and r2 given sm was sent, p(r1, r2|sm), m ∈ (1, 2} and find the error probability as a function of Eb/N0 and θ. For Eb/N0 = 7 dB, plot the bit error probability versus θ for 0 ≤ θ ≤ 2Π.
(d) An alternative (noncoherent) receiver operates by producing two correlator outputs for each frequency:
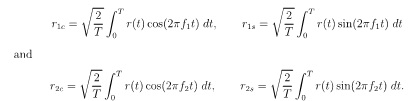
The detector then forms r12 = r1c2 + r1s2 and r22 = r2c2 + r2s2 and picks s1 if r12 > r22 and s2 otherwise.
if the input signal is r(t) = √2Eb/T.cos(2Πfmt +θ) + n(t) then it turns out that if s1 is sent:
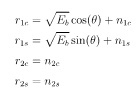
where n1c, n1s, n2c and n2s. are independent and identically distributed Gaussian random variables with mean 0 and variance N0/2.
It is difficult to analytically determine the exact error probability, so instead, you should calculate the error probability using a Monte Carlo simulation in Matlab.For the simulation, set Eb/N0 = 7 dB (set N0 = 1 and Eb = 5) and find the bit error probability for 8 from 0 to 2Π in steps of 0.1.
Compare the result to that obtained in (c). Why is this receiver "robust" to the value of θ?
Please list all of the resources you used to answer this question including references to the subject notes, workshops and problem sets as well as any websites or textbooks etc.
Question 4. Bit Error Rate Calculation with Random C!hannel Gunn The sampled output of a matched-filter is given by
r = hx + n
where the transmitted symbol x = ±√Eb and n is a Gaussian random variable with mean 0 and variance N0/ 2. The channel gain h is known at the receiver and h ≥ 0. Assume the input symbols are equally likely.
(a) Explain the operation of the maximum-a-posteriori (MAP) detector for detecting whether x is -√Eb or √Eb.
(b) Determine an expression for the bit error rate (BER) of the MAP detector in terms of h, Nt and N
(c) Now suppose that h is a discrete random variable that takes values 0.25, 1 and 1.75 with respective probabilities 0.3, 0.4 and 0.3. Determine an expression for the average BER by taking the expected value of the BER expression you obtained in (b).
(d) Plot the average BER from (c) versus Eb/N0 in the range from 0 dB to 20 dB. What happens to this BER as At/N gets large? Can you explain this observation?
(e) Validate your results from (c) by running a Monte-Carlo simulation in MATLAB and plotting the simulated results on top of your plot from
(d). This will involve re- peatedly generating random realisations of z, n and h, forming r, doing the detection and then checking if there is an error.
(f) (Harder) Now suppose that h is a continuous random variable with pdf p(x) = 2x exp( -x2) for x ≥ 0. Again determine an expression for the average BER by taking the expected value of the BER expression in (b). Your initial expression for the average BER might involve an integral of a Q-function. This could be evaluated numerically, but if you work a bit harder you might actually be able to reduce this to a fairly simple closed-form expression. (Hint: Write the Q-function in its integral form and then carefully swap the order of integration.)
(g) Plot the average BER from (I) versus Eb/N0 in the range from 0 dB to 20 dB. What happens to this BER as Eb/N0 gets large?
Please list all of the resources you used to answer this question including references to the subject notes, workshops and problem sets as well as any websites or textbooks etc.
Question 5. Bandlimited Systems and Nyquisl Criterion
Consider a baseband On-Off keying (OOK) system in which the modulator is defined by a symbol interval T and a transmit pulse p(t), the channel is defined by a filter h(t), and the receiver is defined by a filter q(t) which is sampled every T seconds. The received waveform, after the receive filter q(t), is then given by r(t) = ∑jujg(t -jT) where g(t) = p(t)*h(t)*q(t) and {uj} is the transmitted data sequence.
(a) What property must g(t) have so that r(kT) = uk for all k and for all choices of input (uj}? What is the Nyquist criterion for G(f)?
(b) Now assume that T = 1/2 and that p(t), h(t) and q(t) and all their Fourier transforms are restricted to be real. Assume further that P(f) and H(f) are given by
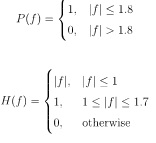
If we choose g(f) to be the raised cosine spectrum, what is the largest possible roll-off factor β. With that β, what is the suitable Q(J)?
(c) Redo question b) with the modification that now H(f) = |f| for |f| ≤ 0.9 and H(f) = 0 for |f > 0.9.
(d) Now consider an OOK bandpass system with the carrier frequency fc = 8 x 103 Hz. Assume this is a digital system and the sampling rate is fs = 2 x 104 Hz, what is the bandwidth of a signal that this system can process without distortion? Then what are the maximum symbol rate that the OOK bandpass system can have?
Please list all of the resources you used to answer this question including references to the subject notes, workshops and problem sets as well as any websites or textbooks etc.
Question 6. (Harder) Multiuser Detection
Consider a multiuser communication system where N-users communicate simultaneously over an additive white Gaussian channel. The kth user is assigned a finite energy signature waveform. sk(t), t∈[0, T], and it transmits data by modulating that waveform antipodally (sending ±sk(t) ). The receiver observes
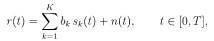
where n(t) is a realization of a white Gaussian process with power spectral density No/2, bk {-1, 1} is the k-th user's data symbol, sk(t) = √2/Tcos(2Πfkt) and fk is the carrier frequency of the k-th user. Let T = 10-2 s and fk = (5 +a (k-1)) 1/T where a is a constant.
Let yk be the output of the demodulator of the k-th user:
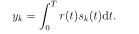
If we write y = [y1,y2....yK]T and b = [b1,b2,....bK]T, then we havey = Hb + n
where H is the crosscorrelation matrix.
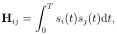
and n is a zero-mean Gaussian vector with covariance matrix equal to N0/2 H.
(a) If K = 1 show that b1 = sign(y1) is the ML detector.
(b) For K = 2, simulate the system using the same detector as in (a) and plot the BER of the two users versus Eb/N0 for different a = (1/8, 1/4, 1/2, 1}and 0 dB ≤ Eb/N0 ≤ 15 dB.
Explain the results that you observe.
(c) Prove that the joint ML detector is
b = arg maxb [2yTb - bTHb]
where b = [b1, b2, ......bk]T are the detected bits for the N users. (Hint: You first need to find the joint likelihood function p(y | b).)
(d) Simulate the system for K = 3 and a = 1/4 using the detectors in (a) and (c). Plot the BERs against Eb/N0 for 0 dB ≤ Eb/N0 ≤ 15 dB.
(e) Since there are 2k possible transmitted bit combinations, the computational com- plexity grows exponentially with N. Thus, different suboptimal detectors with less computational complexity have been proposed. Do a bit of research on multiuser detection to find at least two different suboptimal detectors. Implement one of these and plot the BER to compare its performance with the detectors in (a) and (c). Make sure to compare the complexity of your suboptimal detector to the ML scheme.
Please list all of the resources you used to answer this question including references to the subject notes, workshops and problem sets as well as any websites or textbooks etc.
Question 7. (Harder) The Vilerbi Algorithm
Consider molecular communication using On-Off Keying modulation where no molecules and N molecules are released at the beginning of a symbol interval to transmit bit "0" and "1", respectively. Assume that the two symbols are equiprobable. Let xk and yk denote the numbers of molecules released at the transmitter and received at the receiver in the k-th symbol interval. Due to the random movement of molecules, some molecules released in the k-th interval can arrive in later intervals, causing inter-symbol interference (ISI). The receiver also receives some molecules from a noise source in the environment. Assume that significant ISI is only from one previous symbol and yk follows a Poisson distribution with mean given by
yk = xkp1 + xk-1p2 + n
where n = 1, p1 = 0.15, and p2 = 0.10 are the expected number of noise molecules received in an interval and the probabilities that a molecule released from the transmitter at time zero arrives at the receiver within the first and second symbol intervals, respectively.
Assume that we receive y1,y2 ........y150 and that we wish the determine x1, x2,......x150 Also assume that the first received symbol is not affected by ISI.
(a) Derive the maximum likelihood sequence detector for the system. If your detec- tion involves a product of terms, can you reduce the computational complexity by transforming it to a summation?
(b) Now suppose you wish to implement the maximum likelihood sequence detector from
(a) using the Viterbi algorithm. Sketch the trellis diagram for the first 4 symbol transmissions and specify the states and path lengths, i.e., cost metric functions.
(c) Write Matlab code to implement the Viterbi algorithm on a block of 250 received signals. Test your algorithm by repeatedly generating random +2. and then p , v2, , v running the Viterbi algorithm, and counting the number of errors. Plot the BER versus N for 50 ≤ N ≤ 350.