Reference no: EM13884960

1. Consider the following linear programming model:

Maximize        20x₁  + 30x₂ + 10x₃ + 40x₄

subject    to   2x₁ + 4x2 + 3x₃ + 7x₄  ≤ 10

                    10x₁  + 7x₂  + 20x₃  + 15x₄  ≤ 40

                    x₁ + 10x₂ + x₃ ≤ 10 x₁, x₂, x₃, x₄ binary

Solve this problem using branch-and-bound method. State your node and branching variable selection rules.

2. Kathleen Taylor is a freshman at Roanoke College, and she wants to develop her  schedule for the spring semester. Courses are offered with class periods either on Monday and Wednesday or Tuesday and Thursday for 1 hour and 15 minutes duration, with 15 minutes between class periods. For example, a course designated as 8M meets on Monday and Wednesday from  8:00 A.M. to 9:15 A.M.; the next class on Monday and Wednesday (9M) meets from 9:30 to 10:45; the next class (11M) is from 11:00 A.M.to 12:15 P.M.; and so on. Kathleen wants to take the following   six freshman courses, with the available sections shown in order of her preference, based on the professor who's teaching the course and the time:

Course                                 Sections Available

Math                         11T, 12T, 9T, 11M, 12M, 9M, 81', 8M

History                      11T, 11M, 14T, 14M, 8T, 8M

English                     9T, 11T, 14T, 11M, 12T, I4M, 12M, 9M

Biology                      14T, 11M, I2M, I4M, 9M, Si', 8M

Spanish                    9T, 11M, 12M, 8T

Psychology               14T, 11T, 12T, 9T, 14M, 8M

For example, there are eight sections of math offered, and Kathleen's first preference is the 11T section, her second choice is the 12T section, and so forth. (For each part, a, b, c, write your mathematical model in a word or pdf file and construct excel solver model in excel.)

a. Determine a class schedule for Kathleen that most closely meets her preferences.

Answer the following parts separately.

b. Determine a class schedule for Kathleen if she wants to leave 11:00 A.M. to noon open for lunch every day.

c. Suppose Kathleen wants five of her classes on two days, either Monday and Wednesday or Tuesday and Thursday. Note that all six classes would not fit in one day; at least one class must be scheduled for the other day. Use indicator variable to reformulate the problem to determine a schedule that most closely meets her preferences.

3. A new police car costs the Bay City Police Department $25,000. The annual maintenance cost for a car depends on the age of the car at the beginning of the year. (All cars accumulate approximately the same mileage each year.) The maintenance costs increase as a car ages, as shown in the following table:

Period	Annual Maintenance Cost
1st year	1000
2nd year	4000
3rd year	6000
4th year	8000
5th year	10000

Note that a car cannot be used after 5 years, it should be discarded after 5 years. In order to avoid the increasingly high maintenance costs, the police department can sell a car and purchase a new car at the end of any year. The selling price for a car at the end of each year of use is also shown in the table.

At the end of year	Used Selling Price
1	15000
2	13000
3	10000
4	7000
5	2000

It is assumed that the price of a new car will increase $500 each year. The department's objective is to develop a car replacement schedule that will minimize total cost (i.e., the purchase cost of a new car  plus maintenance costs minus the money received for selling a used car) during the next 6 years (until the end of year 6). Develop a car replacement schedule, using the shortest route method.

4. A developer is planning a development that includes subdivisions of houses, cluster houses, townhouses, apartment complexes, shopping areas, a daycare center and playground, a community center, and a school, among other facilities. The developer wants to connect the facilities and areas in the development with the minimum number of streets possible. The following network shows the possible street routes and distances (in thousands of feet) between 6 areas in the development that must be connected:

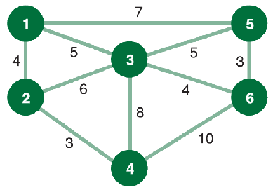
a. Determine a network of streets to connect the 6 areas with minimum length, and indicate the total streets (in thousands of feet) needed using the method we have seen in class (without using any optimization software).

b. Formulate an integer (or binary) programming model to determine a network of streets to connect the 6 areas with minimum length and optimize with excel solver (Please do not forget to submit your excel solver model via Blackboard).

5. The Dynaco Company manufactures a product in five stages. Each stage of the manufacturing process is conducted at a different plant. The following network shows the five different stages and the routes over which the partially completed products are shipped to the various plants at the different stages:

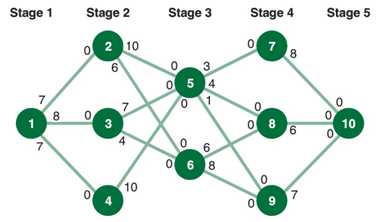
Stage 5 (at node 10) is the distribution center in which final products are stored. Although each node represents a different plant, plants at the same stage perform the same operation. (For example, at  stage 2 of the manufacturing process, plants 2, 3, and 4 all perform the same manufacturing operation.) The values accompanying the branches emanating from each node indicate the maximum number of units (in thousands) that a particular plant can produce and ship to another plant at the next stage. (For example, plant 3 has the capacity to process and ship 7,000 units of the product to plant 5.)

a. Determine the maximum number of units that can be processed through the five-stage manufacturing process and the number of units processed at each plant by the method we have seen in class (without using any optimization software). Show the paths you selected/evaluated at each step (you do not need re-draw the network).

b. Suppose that the processing cost per unit at each plant is different because of different machinery, workers' abilities, overhead, and so on, according to the following table:

Stage 1	Stage 2	Stage 3	Stage 4
1. $3	2. $5	5. $21	7. $11
	3. $8	6. $18	8. $14
	4. $4		9. $15

There are no differentiated costs at stage 5, the distribution center. Assume that production and shipments can be made in multiples of 1000. Given a budget of $650,000, formulate an integer programming model to determine the maximum number of units that can be processed through the five-stage manufacturing process and solve by excel solver. What is the solution if you ignore the integrality constraints? Why do you think you need to include integrality constraints for this maximal flow problem?