Reference no: EM131607

You are to design and FIR filter where the filter coefficients are the following numbers: 3323939

Therefore, the difference equation is as follows:

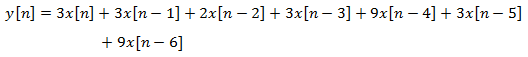
And here is the impulse response of this FIR filter.

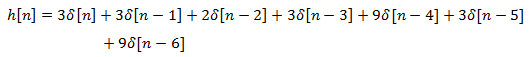
The z-transform of this FIR filter will be:

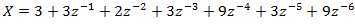
Use Matlab to find the roots of this FIR filter and use zplane() function to plot the location of poles and zeros. Also, use MATLAB to plot the frequency and phase response of this FIR filter using freqz() function.

I've answered this as you see below; please correct me if I'm wrong (you should have the matlab file that I've uploaded to you).

The roots of the FIR filter are as follows:

r =

  -1.2278 + 0.7715i

  -1.2278 - 0.7715i

   0.8300 + 0.9374i

   0.8300 - 0.9374i

  -0.1022 + 0.9485i

  -0.1022 - 0.9485i

Using zplane() function, the location of poles and zeros are as follows:

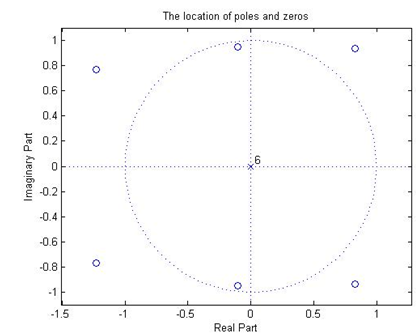
The frequency response and phase response of the FIR filter are

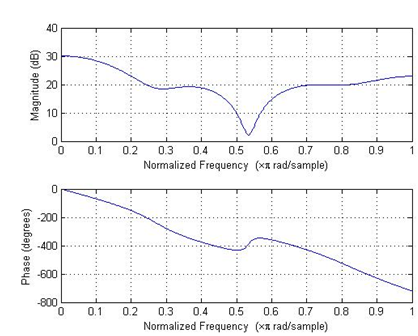
The following questions are the most important ones for me; answering them correctly is important.

Discussion:

1. What does the pole-zero (z-plane) diagram tells you about the filter?

2. Is the filter stable or unstable?

3. What can you tell about the filter from its frequency and phase response? Discuss how the filter would respond to different input signal frequencies (does it null out certain frequencies? Does it act as lowpass or  highpass filter? Is it none of the above?).