Reference no: EM13974737

Question 1. Given a graph G = (V, E) where |V| = n and |E| = m, let A ⊂ V be a subset of the vertices. A cut is the number of edges in the graph with one endpoint in A and one endpoint in V - A. In class we saw a randomized algorithm to compute a min-cut, which is a cut whose size is minimum over all possible cuts (i.e. over all possible subsets A). For this question, we are interested in computing a max-cut, which is a cut whose size is maximum over all possible cuts. It is known that computing a max-cut in a graph is NP-Hard. As such, we will find an approximate solution whose size is at least 1/2 the optimal size.

Consider the following simple algorithm:

Algorithm ApproxMaxCut(G=(V,E))
Let A be a random subset of V (where each subset of V is equally likely).

Let B = V-A.

Output C = all edges of E with one endpoint in A and one endpoint in B

(a) For a vertex x ∈ V , prove that P (x ∈ A) = 1/2.

(b) Prove that the expected number of edges in C is |E|/2.

(c) Explain why this is a 1/2 approximation of the optimal maximum cut?

Question 2. Suppose you have access to a function Rand(i) that returns an integer uniformly distributed in the set {0 . . . , i}. Subsequent calls to the function produce independent results. Starting with an array A containing the elements 1, . . . , n in sorted order show how to compute a random permutation of A in O(n) time. Note, you must prove that the permutation generated by your algorithm is random. I.e., you must prove that each of the n! possible permutations is equally likely.

Question 3. Let a = (a₁, . . . , a_n) and b = (b₁, . . . , b_n) be two real-valued vectors of length n and let r = (r₁, . . . , r_n) be a random binary vector of length n. That is, the ri^'s are chosen independently and uniformly at random to be either 0 or 1. For a vector x, let r.x denote the sum r₁x₁ + r₂x₂ + . . . + r_nx_n.

(a) If a = b then r.a = r.b. Show that if a ≠ b then P_r(r.a = r.b) ≤ 1/2.

(Hint: Consider what has to happen at a particular index i such that a_i ≠ b_i. What is the probability that this happens?)

(b) Using the above fact (whether you could provide a proof or not), show that for two n× n matrices A and B that are not equal, P_r(A_r = B_r) ≤ 1/2. (Note that A_r is an n vector that takes O(n²) time to compute.)

(c) Let A, B and C be three n × n matrices. Describe an algorithm that runs in O(n²) time and (a) If A = B × C then the algorithm always outputs yes. (b) If A ≠ B × C then the algorithm will output no with probability at least 1/2. (Hint: Matrix multiplication, i.e., computing B × C explicitly takes too long. You'll have to find some other way.)

Question 4. Given a set P of n points in the plane, compute the pair of points x, y ∈ P such that d(x, y) ≥ d(a, b) for all pairs of points a, b ∈ P . In other words, x, y is the furthest pair. Use the following two routines as black boxes in the design of your algorithm. Given a set D of n disks, I(D) returns the intersection of these n disks in O(n log n) time. Given a point p, and I(D), the routine C(p, I(D)) determines in O(log n) time whether p ∈ I(D).

(a) Design a simple randomized algorithm to find the furthest pair in O(n log n) expected time.

(b) Explain why it is correct.

(c) Explain why the running time is O(n log n) expected time.

Question 5. Let P be a set of n points uniformly distributed in the unit square. This means that each point p_i = (x_i, y_i) where x_i and y_i are uniformly distributed on the interval [0, 1]. A point is called right- empty if there are no other points in its upper right quadrant.

In other words, p_i is right-empty if ∀p_j ∈ {P - p_i} we have x_j < x_i or y_j < y_i. In the figure below, the bold points are right-empty. The empty right quadrant is shaded for one of the points.

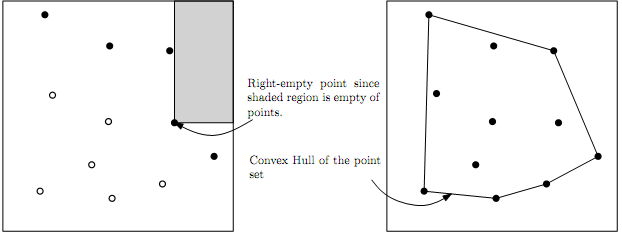
(a) Show that the expected number of right-empty points is O(log n).

(b) The convex hull of a point set is the smallest convex polygon that contains the point set. Use the above result to show that the expected number of points on the convex hull is O(log n).

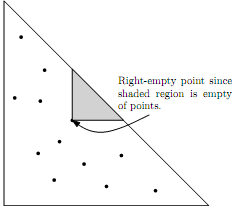
Question 6. BONUS CHALLENGE QUESTION (Not required and only do if you have time): Instead of points uniformly distributed in the unit square, consider n points uniformly distributed in a triangle defined by vertices (0, 0), (1, 0), (0, 1). Give an upper bound on the expected number of right-empty points.

(Hint: The bound is much larger than log n. Try for a bound of √n. Anything that is o(n) is good.).